Quench dynamics in integrable atomic systems
The Art of Mathematical Physics
in honour of Hubert Saleur
Institut de Physique Théorique, CEA Saclay22 September 2021
Jean-Sébastien Caux




Château de Brézé

Château de Brézé

Château de Brézé
Plan of the talk
The Lieb-Liniger Model
$ H = \int_0^L dx \left[ \partial_x \Psi^{\dagger}(x) \partial_x \Psi(x) + c \Psi^{\dagger} (x) \Psi^{\dagger}(x) \Psi(x) \Psi(x) \right] $
Bethe equations:
$ e^{\mathrm{i}\lambda_j L} = \prod_{l \neq j}\prod_{\substack{l=1 \\ l\neq j}}^N \frac{ \lambda_j - \lambda_l + \mathrm{i}c}{\lambda_j - \lambda_l - \mathrm{i}c} $
Eigenvalues of conserved charges:
$ Q_n\left(\{\lambda\}_N\right) = \sum_{j=1}^N \lambda_j^n, \quad n = 1,2,\ldots $
with in particular $P = Q_1, E = Q_2$.
Dynamical structure factor
from (algebraic) Bethe Ansatz
The ABACUS algorithm
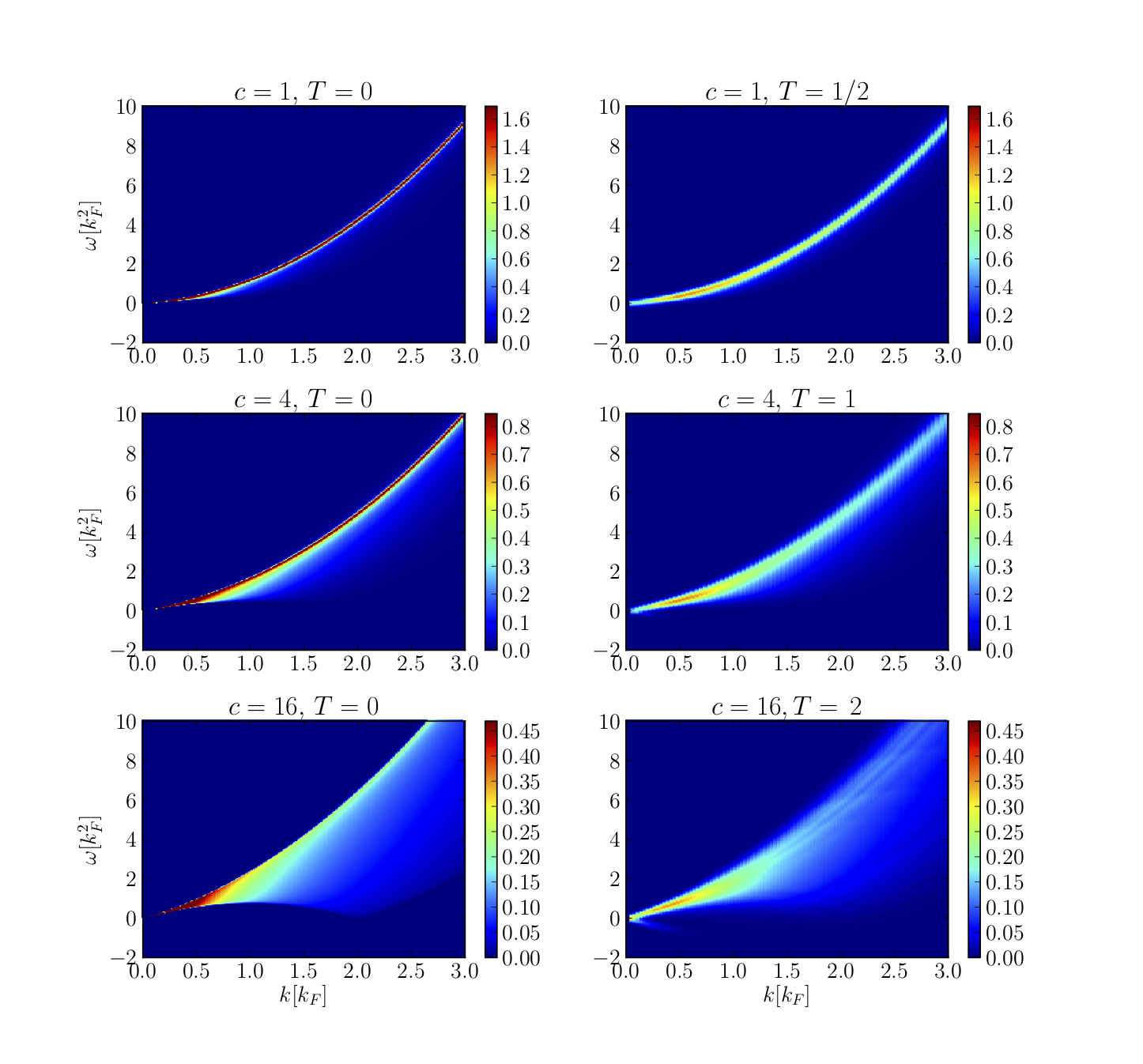
Dynamical structure factor from Bethe Ansatz
extension to finite TM. Panfil and J-SC, PRA 89 (2014)
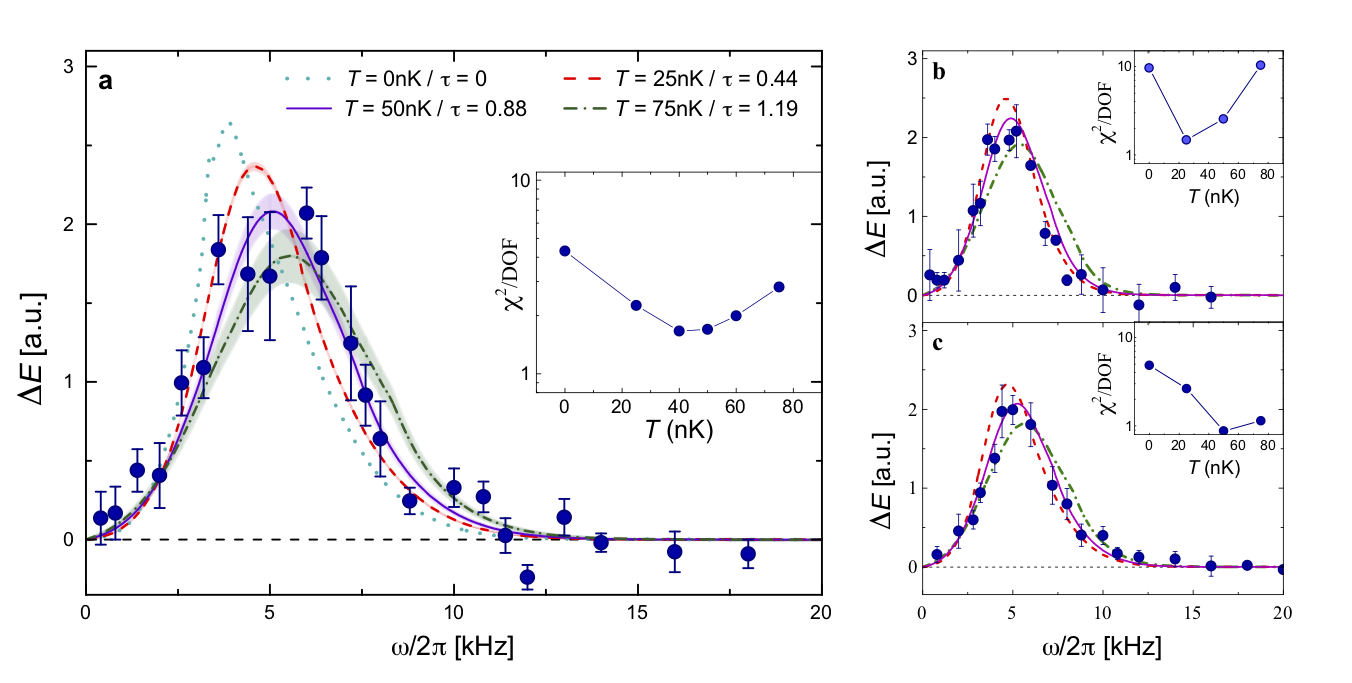
Lieb-Liniger using cold atoms (I)

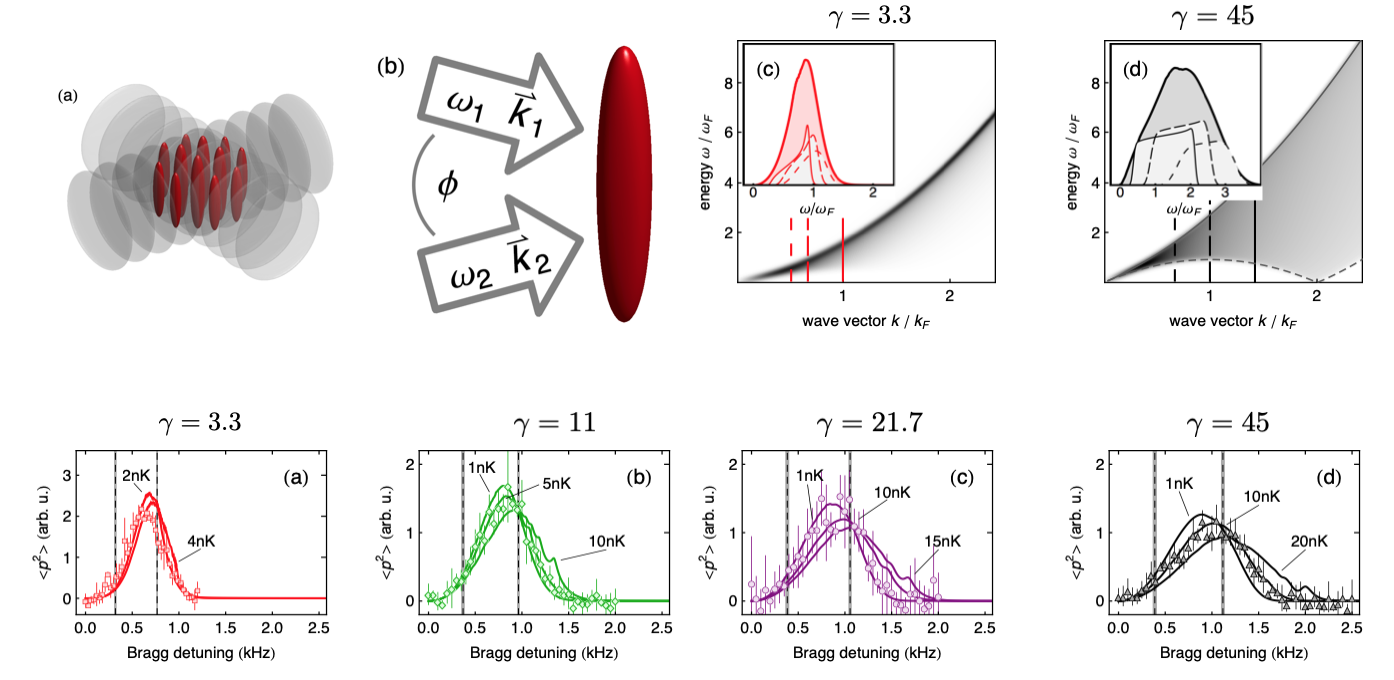
Lieb-Liniger using cold atoms (II)

What we really would like to do with exact methods
- Beyond linear response
- Quenches
- Driving
Out-of-equilibrium using Integrability
- The super Tonks-Girardeau gas
- Split Fermi seas (Moses states)
- Spin echo in quantum dots
- Quasisolitons
- Interaction quench in Richardson
- Domain wall release in Heisenberg
- Geometric quench
- Interaction cutoff in Lieb-Liniger
- Release of trapped Lieb-Liniger
- BEC to Lieb-Liniger quench
- Quantum Newton’s Cradle in TG
- Néel to XXZ quench
- Generalized hydrodynamics
- Floquet driven spin chains
Quenches
Interaction quench in Lieb-Liniger
We will consider a sudden switch of the interaction:
$ c (t) = \left\{ \begin{array}{ll} c_i & t < 0, \\ c_f & t > 0 \end{array} \right. $
starting in ground/(any eigen)state of $H(c_i)$ at $t < 0$
For many reasons, this is a complicated problem...
- GGE logic fails, charges have $\infty$ exp. values
- approaches using regularizations (q-bosons, extended charges, ...): no complete solution
The strategy
We write the initial state in the basis of the eigenstates of $H(c_f)$, denoted as $\left\{ |\{\lambda\}^{(n)}_N\rangle \right\}, n = 0, 1, ...$
The initial state is obtained as a linear decomposition weighed by exact overlaps:
$ |\Psi_i\rangle = \sum_{n=0}^\infty |\{\lambda\}^{(n)}_N\rangle \underbrace{\langle \{\lambda\}^{(n)}_N | \Psi_i\rangle}_{\text{the overlaps}} $
Exact time-evolved state:
$ |\Psi_i(t)\rangle \equiv e^{-iH(c_f)t} |\Psi_i\rangle = \sum_{n=0}^\infty e^{-\mathrm{i}E(\{\lambda\}^{(n)}_N)t} |\{\lambda\}^{(n)}_N\rangle \langle \{\lambda\}^{(n)}_N | \Psi_i\rangle $
The Quench Action
Setup
The initial state is decomposed in the basis of post-quench Hamiltonian eigenstates:
$ |\Psi (t=0) \rangle = \sum_{\{ I \}} e^{-S^\Psi_{\{ I \}}} | \{ I \} \rangle, $
with overlaps encoded in the coefficients$ S^\Psi_{\{ I \}} = -\ln \langle \{ I \} | \Psi (t=0) \rangle ~\in ~\mathbb{C} $
Exact time-dependend expectation values:
$ \bar{\cal O} (t) = \frac{ \sum_{\{ I^l \} } \sum_{\{ I^r\}} e^{-(S^\Psi_{\{ I^l\}})^* - S^\Psi_{\{ I^r\}} + i (\omega_{\{ I^l\}} - \omega_{\{ I^r\}})t} \langle \{ I^l \}| {\cal O} | \{ I^r \} \rangle}{\sum_{\{ I \}} e^{-2\Re S^\Psi_{\{ I \}}}} $
Going to the thermodynamic limit
Summations over eigenstates are replaced by functional integrals
$ \lim_{Th,reg} \sum_{\{ \rho_i \}} (...) = \int_{\rho_{sm} \in C^\infty} D\rho_{sm} (...) $
Normalization sum (trivially 1) represented as
$ \lim_{Th,reg} \langle \Psi (t) | \Psi (t) \rangle = \int D\rho_{sm} ~ e^{-S^Q[\rho_{sm}]} $
where the Quench Action is defined as
$ S^{Q}[\rho] = S^o[\rho] - S^{YY}[\rho] $
Time-dependent expectation values
In ThLim, saddle-point evaluation $\left. \frac{\delta S^Q[\rho]}{\delta \rho} \right|_{\rho_{sp}} = 0$ exactly gives the full time evolution of observables as
$ \begin{align} \lim_{Th,reg} \bar{\cal O} (t) = \lim_{Th,reg} \frac{1}{2} \sum_{\bf e} \left[ e^{-\delta S_{\bf e}[\rho_{sp}] - i \omega_{\bf e}[\rho_{sp}] t} \langle \rho_{sp} | {\cal O} | \rho_{sp}; {\bf e} \rangle \right. \nonumber \\ \left. + e^{-\delta S^*_{\bf e}[\rho_{sp}] + i \omega_{\bf e}[\rho_{sp}] t} \langle \rho_{sp}; {\bf e} | {\cal O} | \rho_{sp} \rangle \right] \end{align} $
provided the
operator ${\cal O}$ is
- weak
- smooth
- thermodynamically finite
The BEC to Lieb-Liniger quench
Initial state: ground state of free bosons
$ | \Psi_0 \rangle = \frac{1}{\sqrt{L^N N!}} \left(\psi_{k=0}^\dagger\right)^N | 0 \rangle $
Exact overlaps with finite $c$ Lieb-Liniger states:
$ \langle \Psi_0 | \{ \lambda \}_{N/2} \cup \{ -\lambda \}_{N/2} \rangle = \left[ \frac{(cL)^{-N} N!}{\mbox{det}_N G_{jk} }\right]^{1/2} \frac{\mbox{det}_{N/2} G^Q_{jk}}{\prod_{j=1}^{N/2} \frac{\lambda_j}{c} \left[ \frac{\lambda_j^2}{c^2} + \frac{1}{4} \right]^{1/2}} $
in which $G_{jk}$ is the Gaudin matrix
$ G_{jk} = \delta_{jk} \left[ L + \sum_{l=1}^N K (\lambda_j, \lambda_l) \right] - K(\lambda_j, \lambda_k) $
Exact solution using Quench Action
$ S^Q = L\int_0^\infty d\lambda \rho(\lambda) \log\left(\frac{\lambda^2}{c^2} \left( \frac{1}{4} + \frac{ \lambda^2}{c^2} \right) \right) + S^{YY} $
Saddle-point equation:
$ \ln \eta(\lambda) = g(\lambda) - h - \int_{-\infty}^\infty \frac{d\lambda'}{2\pi} K (\lambda - \lambda') \ln \left[ 1 + \eta^{-1}(\lambda') \right], $
with driving term $ g(\lambda) = \ln \left[ \frac{\lambda^2}{c^2} \left( \frac{\lambda^2}{c^2} + \frac{1}{4} \right) \right] $
Analytic solution for steady state:
$ \begin{align} \rho_{sp} (\lambda) &= -\frac{\gamma}{4\pi} \frac{1}{1 + a(\lambda)} \frac{\partial a(\lambda)}{\partial \gamma},\\ a(\lambda) &\equiv \frac{2\pi}{\frac{\lambda}{n} \sinh \frac{2\pi \lambda}{c}} I_{1 - 2i\frac{\lambda}{c}} \left(\frac{4}{\sqrt{\gamma}}\right) I_{1 + 2i\frac{\lambda}{c}} \left(\frac{4}{\sqrt{\gamma}}\right) \end{align} $
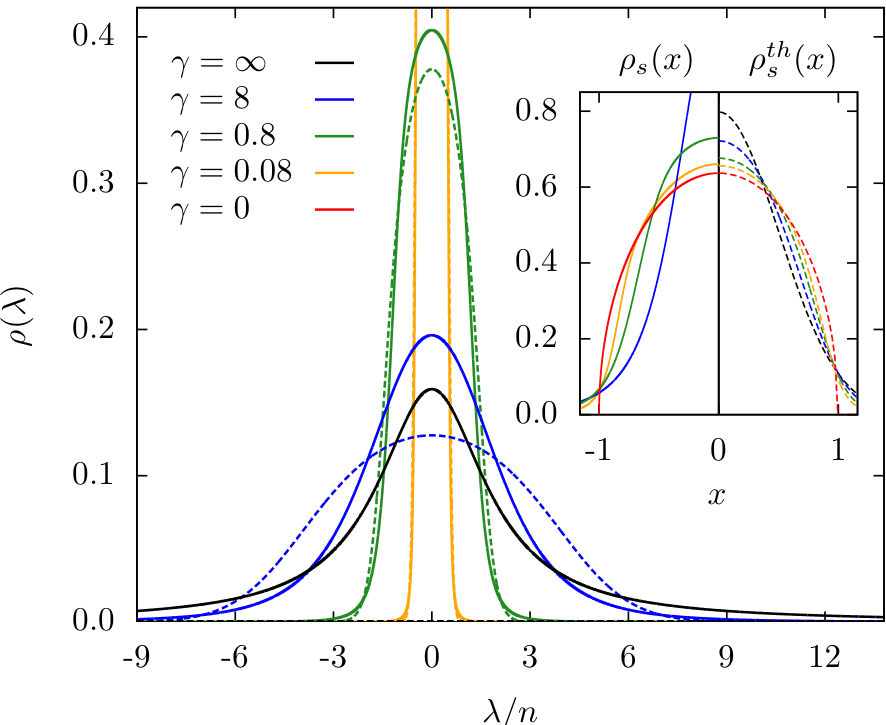
Exact solution using Quench Action
Steady state distribution: non-thermal
J. De Nardis, B. Wouters, M. Brockmann & J-SC, PRA 89, 2014
Numerical Renormalization approach
to interaction quench
in Lieb-Liniger
Neil Robinson, Bart de Klerk + JSC
Viewed as a perturbation
$ H(c_i) = H(c_f) + (c_i - c_f) \int_0^L dx \Psi^\dagger(x)\Psi^\dagger(x)\Psi(x)\Psi(x) $
Matrix elements of the original Hamiltonian in the computational basis of post-quench eigenstates:
$ \begin{align} \langle \{\lambda\}^{(m)}_N | H(c_i) | \{\lambda\}^{(n)}_N \rangle &= \delta_{n,m} E\big(\{\lambda\}^{(n)}_N \big) + \\ &+ (c_i - c_f) L\, \langle \{\lambda\}^{(m)}_N | \big(\Psi^\dagger(0)\big)^2 \big( \Psi(0) \big)^2 |\{\lambda\}^{(n)}_N\rangle \end{align} $
Said otherwise, we perturb the system with the operator
$ g_2(0) = \big( \Psi^\dagger(0)\big)^2 \big(\Psi(0)\big)^2 $
Truncated Spectrum Approach
Idea: truncate Hilbert space to low-E sector using cutoff $\Lambda$, then diagonalize numerically
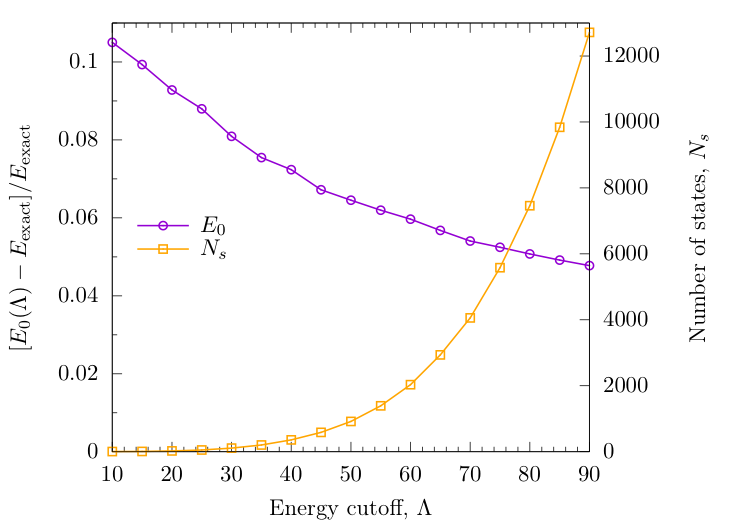
NRG + TSA
The overall workflow:
- Construct the computational basis $\{ |\{\lambda\}^{(j)}\rangle\}$ and order by energy $E(\{\lambda\}^{(j)})$
- Construct the Hamiltonian with the lowest $N_s+\Delta N_s$ states: $ \begin{align} \Big\{ |\{\lambda\}^{(1)}\rangle, \ldots, |\{\lambda\}^{(N_s+\Delta N_s)}\rangle\Big\}, \end{align} $ and diagonalize it, obtaining approximate energies and eigenstates $ \begin{align} \Big\{ |E^{(1)}\rangle, \ldots , |E^{(N_s+\Delta N_s)}\rangle \Big\}. \end{align} $
- Discard the highest $\Delta N_s$ approximate eigenstates $ \begin{align} \Big\{|E^{(N_s+1)}\rangle,\ldots,|E^{(N_s+\Delta N_s)}\rangle\Big\}, \end{align} $ and form a new basis with the lowest $N_s$ approximate eigenstates and the next $\Delta N_s$ lowest states in the computational basis.
- Construct the Hamiltonian in the new basis, and diagonalize to obtain new approximate eigenstates.
- Return to the third step.
Harmonically trapped Lieb-Liniger
JSC & R. M. Konik, Phys. Rev. Lett. 109, 175301 (2012)
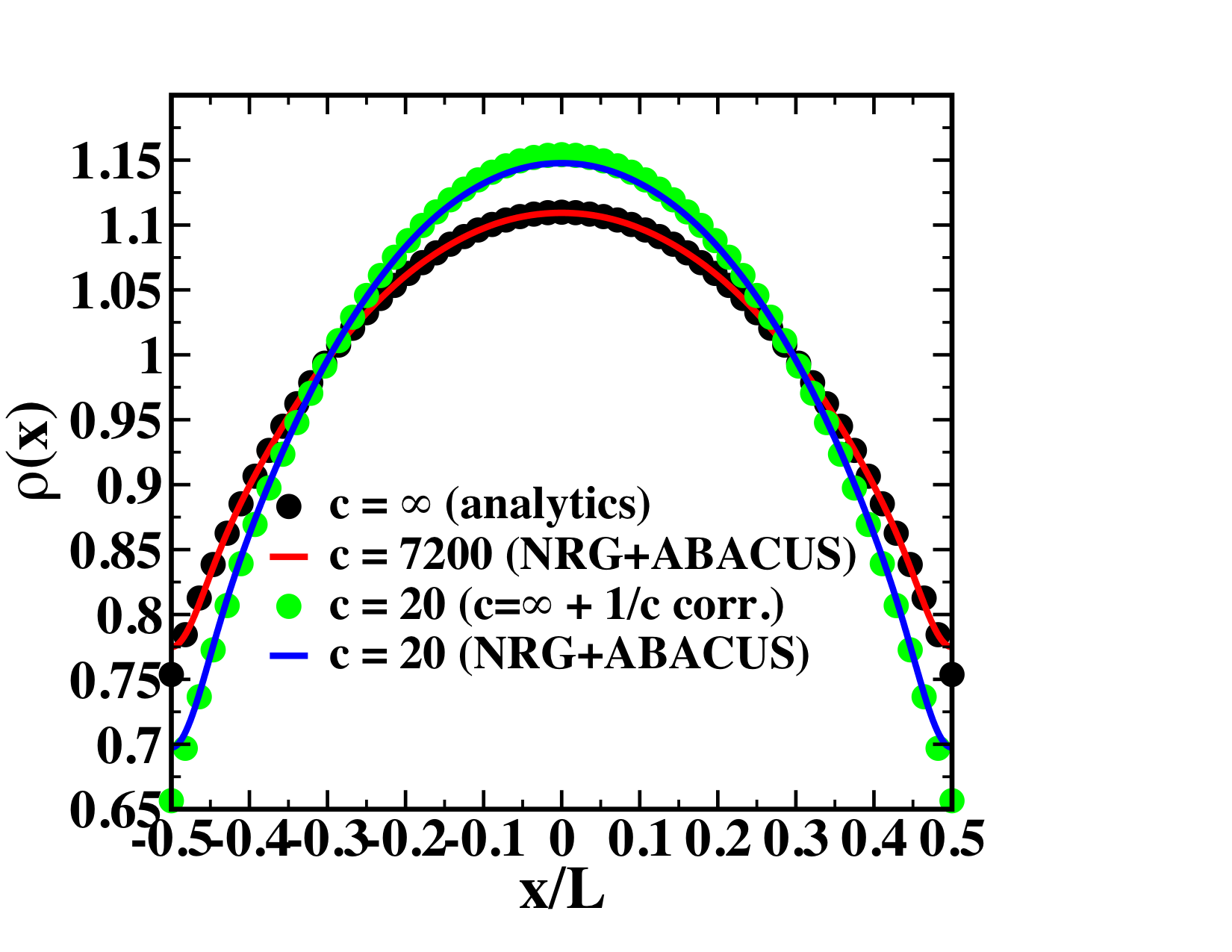
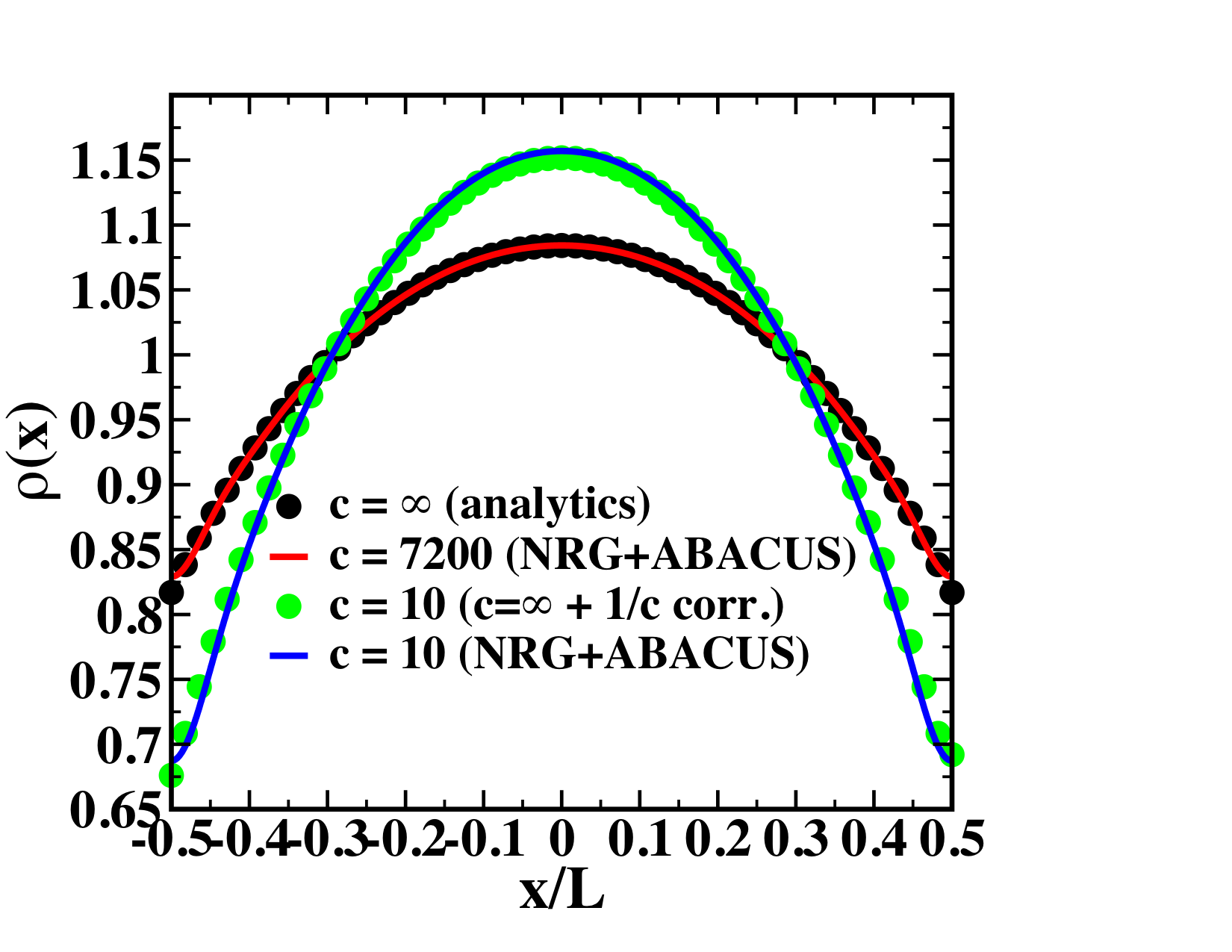
Interaction quench: GSE from NRG + TSA
Neil Robinson, Bart de Klerk + JSC, to appear in SciPost Physics
Ground-state energy from NRG + TSA
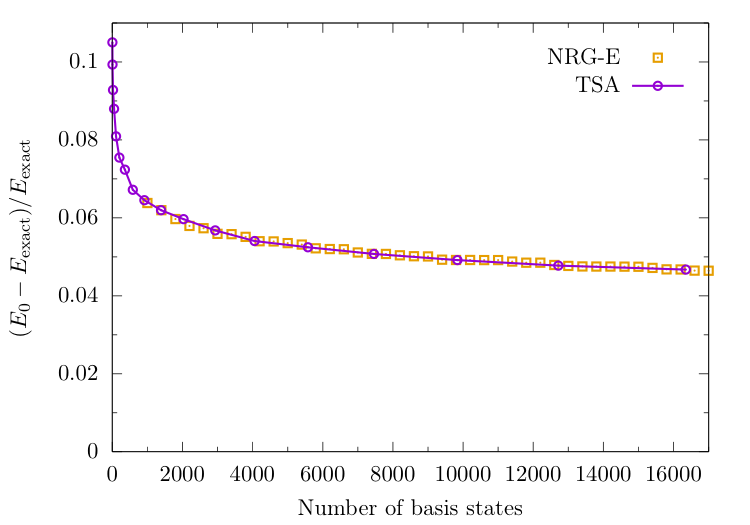
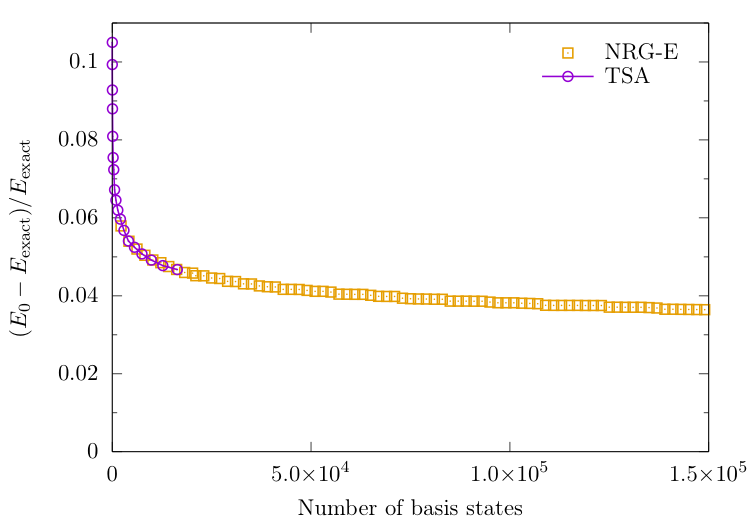
$N_s=600$ and $\Delta N_s = 200$ (corresponding to an initial energy cutoff of $\Lambda \approx 50$)
NRG follows TSA, but can include many more states.
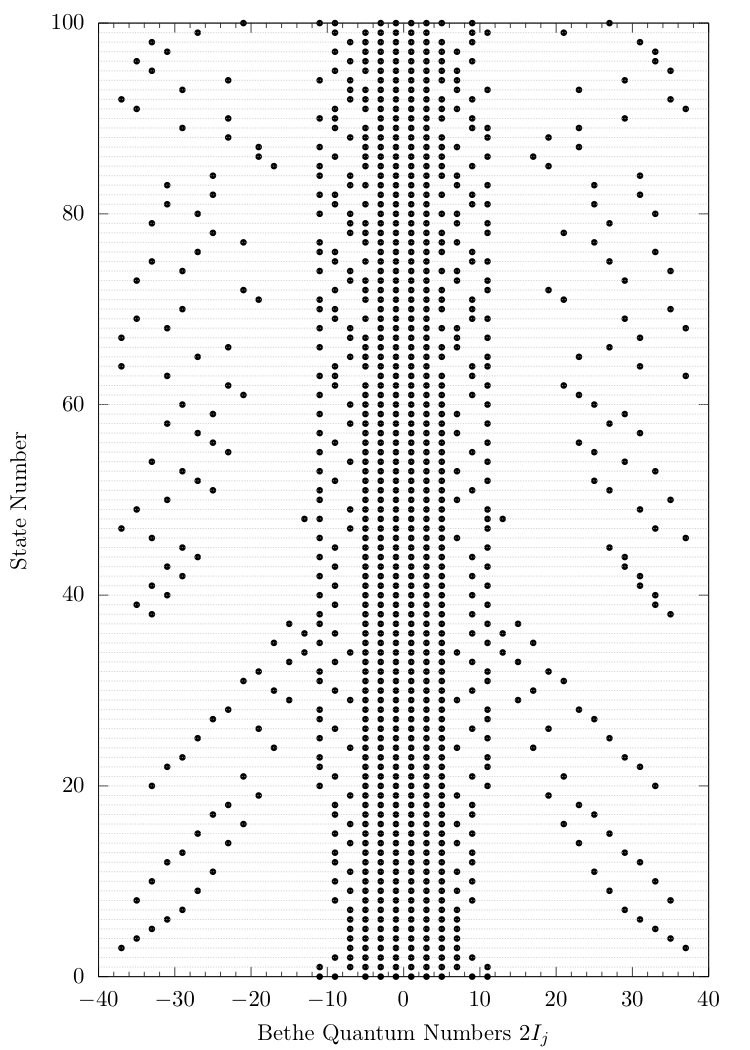
Is ordering in energy a good idea?
Let's try an alternative metric...
We will order by matrix element size, between states in computational basis and the 3 lowest-lying ones from TSA:
$ \left| \langle \{\lambda\}^{(n)}_N | g_2(0) | \tilde E_j\rangle \right|, ~~j =0,1,2. $
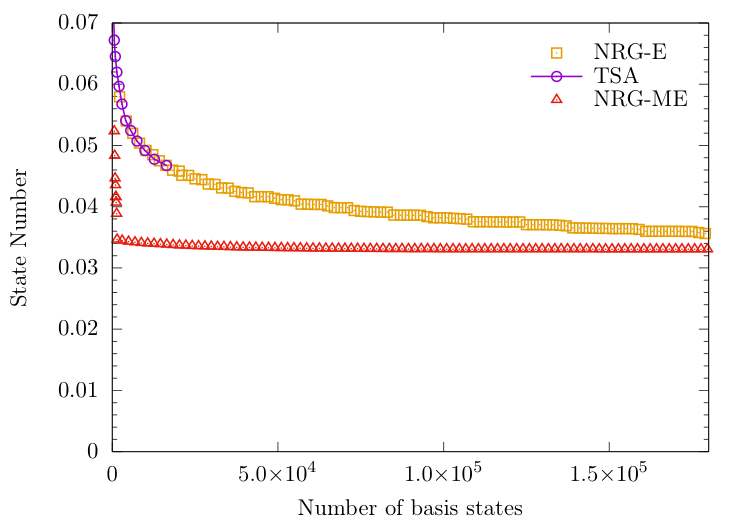
NRG-E versus NRG-ME
Energy ordering versus Matrix Element ordering
NRG-ME: convergence of the overlaps
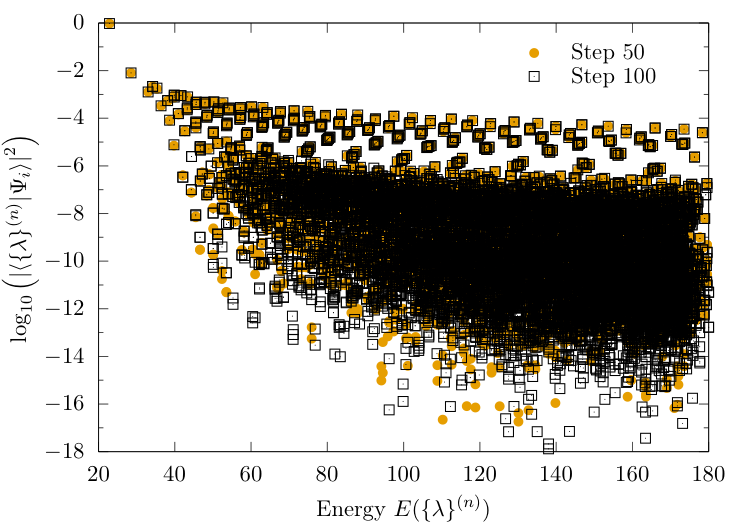
Highest overlap states

Earlier ME ordering

Towards a "perfect" ordering
ABACUS is really efficient at computing
dynamical correlation functions
For an operator ${\cal O}$, it preferentially seeks states with high matrix elements $ \langle \{\lambda\}^{(0)}_N | {\cal O} | \{\lambda\}^{(n)}_N\rangle $
Strategy: use ABACUS idea but with metric
$ w\left(|\{\lambda\}^{(n)}_N\rangle\right) = \left\vert \frac{\langle \{\lambda\}^{(n)}_N | g_2(0) | \{\lambda\}^{(0)}_N\rangle}{ E(\{\lambda\}^{(n)}_N) - E(\{\lambda\}^{(0)}_N) + \epsilon}\right\vert $
which favours the lower end of the spectrum
($\epsilon$ is set to $0.1$ to avoid $(n)=(0)$ divergence)
Preferential ordering
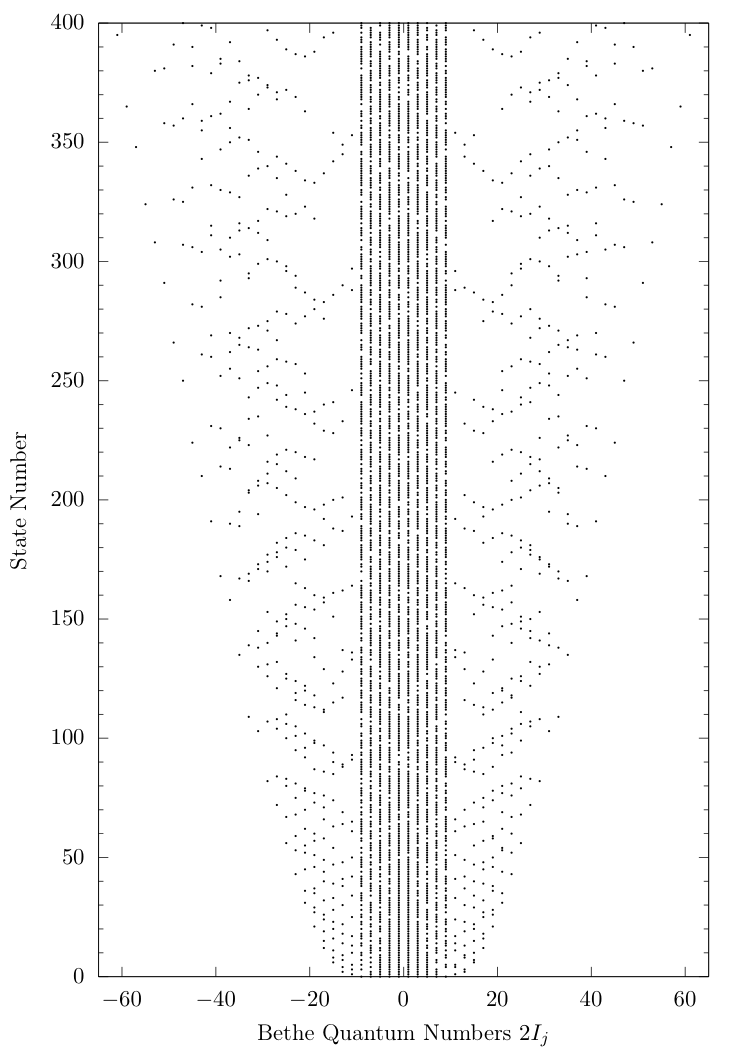
This produces an ordering which is similar to the "back-engineered" one from the overlaps:

Energy convergence
using "optimal" ordering
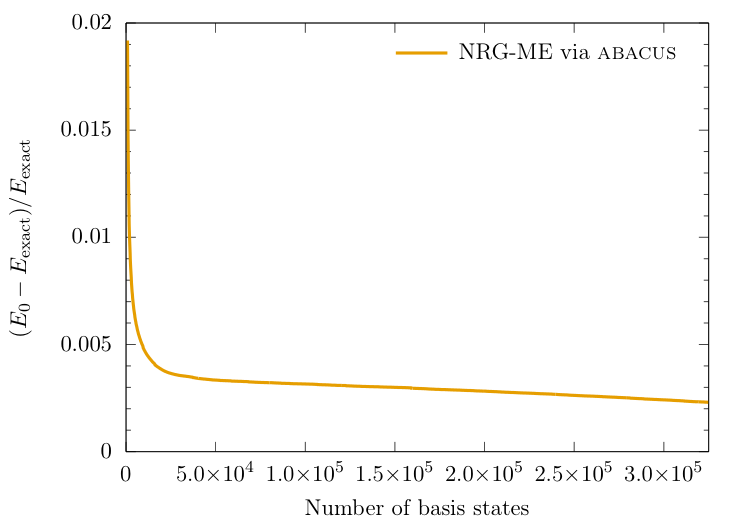
- ABACUS short run
- 390K states generated
- preferentially ordered
- NRG performed with $N_{NRG}=800$ and $\Delta N = 160$
- Convergence of $E_0$ to under 1% achieved with only a few thousand basis states
Real-time dynamics after the quench
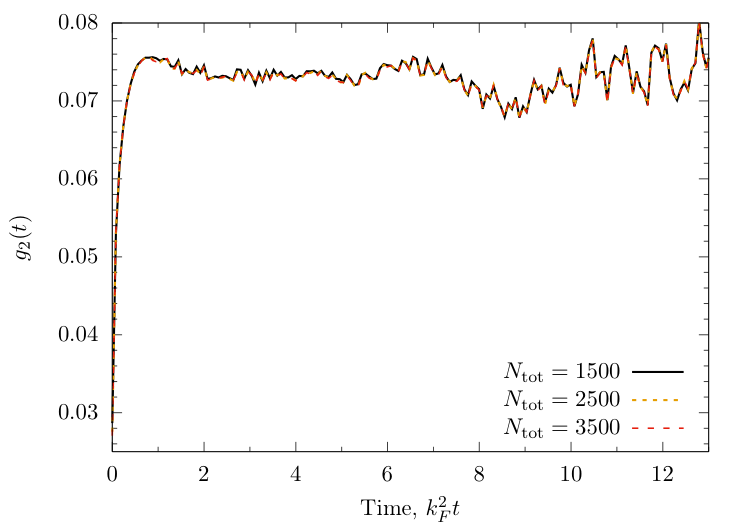
Return amplitude
$ \langle \Psi_i |\Psi_i(t)\rangle \approx \sum_{n=0}^{N_{\text{tot}}} e^{-\mathrm{i}E(\{\lambda\}^{(n)}t} \left\vert \langle \{\lambda\}^{(n)} | \Psi_i \rangle \right\vert^2 $
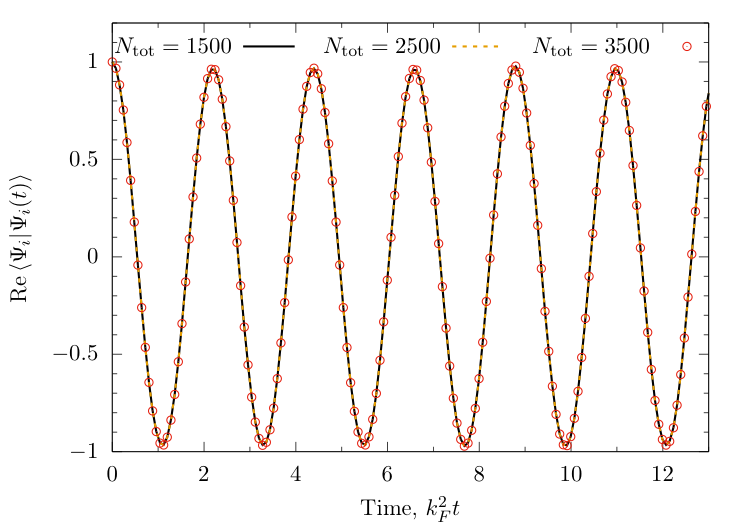
Fidelity
$ {\cal F}(t) = |\langle\Psi_i|\Psi_i(t)\rangle|^2 $
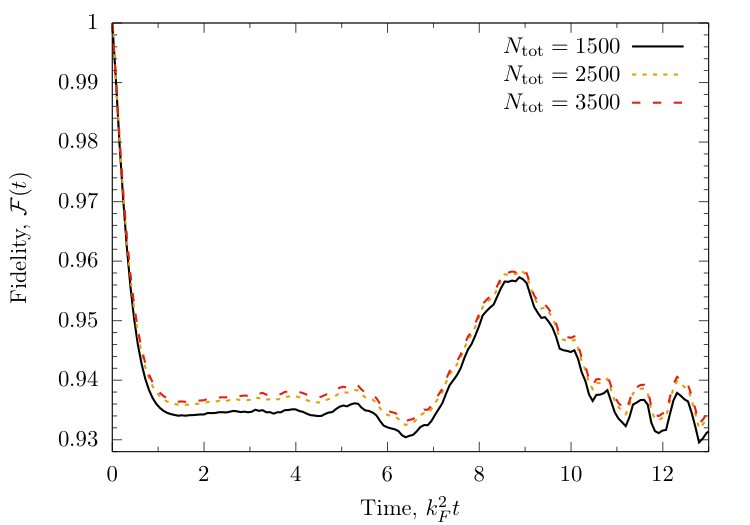
Time dependence of local observables
$ \begin{align} \langle &O(t)\rangle_i \equiv \langle \Psi_i(t) | O |\Psi_i(t)\rangle\\ & = \sum_{n,m=0}^{N_\text{tot}} e^{-\mathrm{i}t[E(\{\lambda\}^{(n)}) - E(\{\lambda\}^{(m)})]} \langle \Psi_i | \{ \lambda \}^{(m)} \rangle \langle \{ \lambda \}^{(m)} | O |\{\lambda\}^{(n)} \rangle \langle \{\lambda\}^{(n)} | \Psi_i\rangle \end{align} $
Generalized Hydrodynamics
Quenches from spatially inhomogeneous states
- B. Bertini, M. Collura, J. De Nardis and M. Fagotti, PRL 117, 207201 (2016)
- O. A. Castro-Alvaredo, B. Doyon and T. Yoshimura, PRX 6, 041065 (2016)
- B. Doyon and T. Yoshimura, SciPost Phys. 2, 014 (2017)
After initial dephasings: 'hydrodynamic' evolution described by local GGE
$\partial_t \rho (\lambda) + \partial_x (v^{\tiny \mbox{eff}}(\lambda) \rho (\lambda)) = 0$
with effective velocities determined by the dressing equation
Effective dynamics:
"flea gas" of scattering quasiparticles
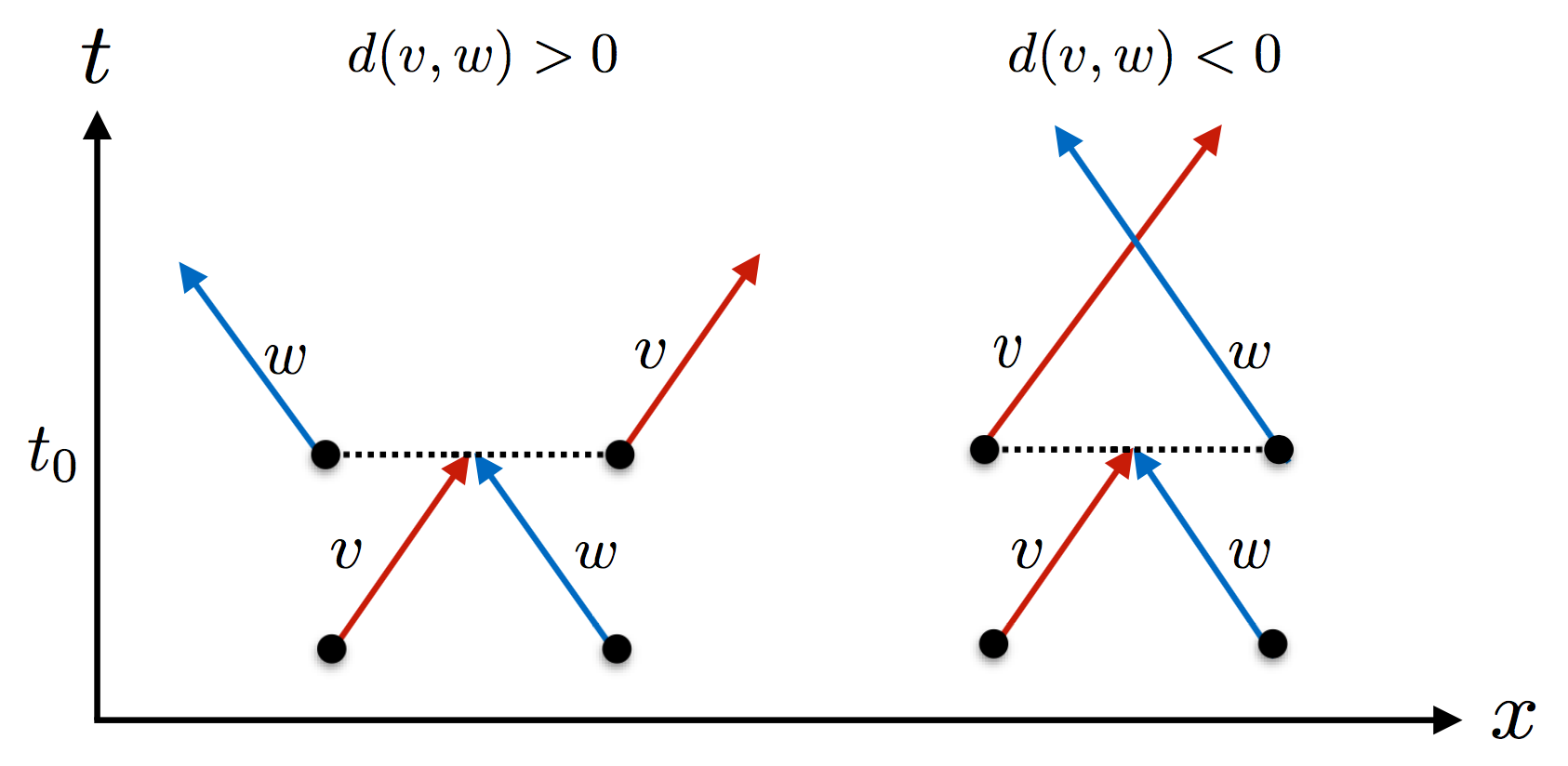
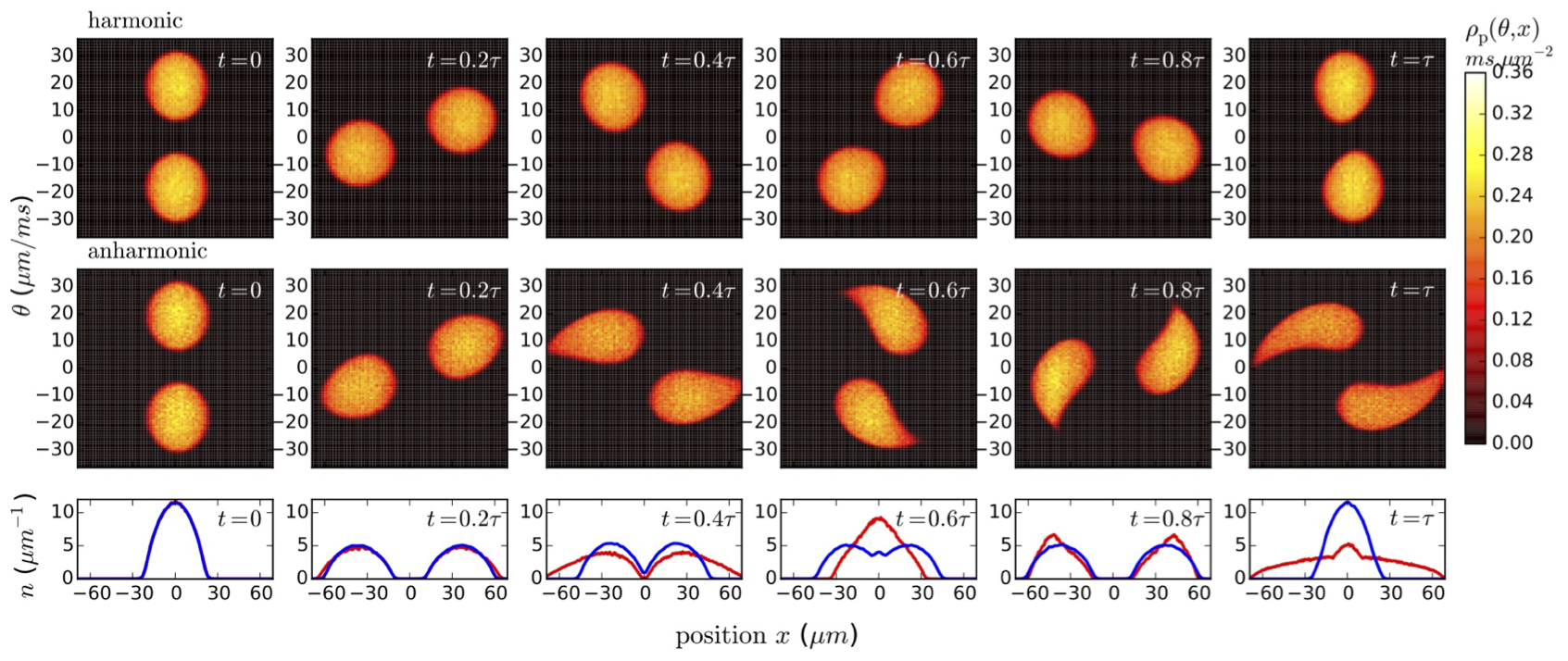
Flea gas GHD
for the Quantum Newton's Cradle
JSC, B. Doyon, J Dubail, R. Konik and T. Yoshimura, SciPost Phys. 6, 070 (2019)
Short time scales:
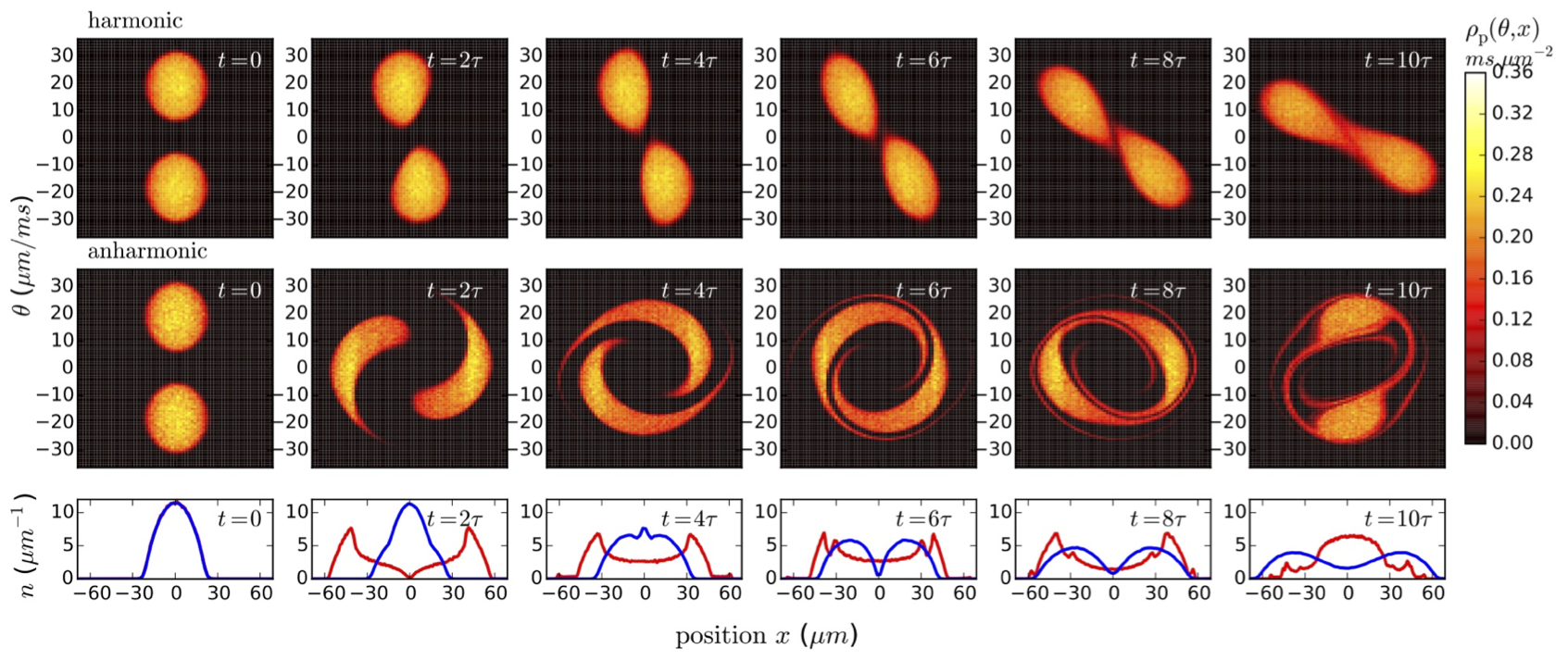
Flea gas GHD
for the Quantum Newton's Cradle
JSC, B. Doyon, J Dubail, R. Konik and T. Yoshimura, SciPost Phys. 6, 070 (2019)
Longer time scales:
Generalized Hydrodynamics with space/time-dependent potentials
Phys. Rev. Lett. 123, 130602 (2019)


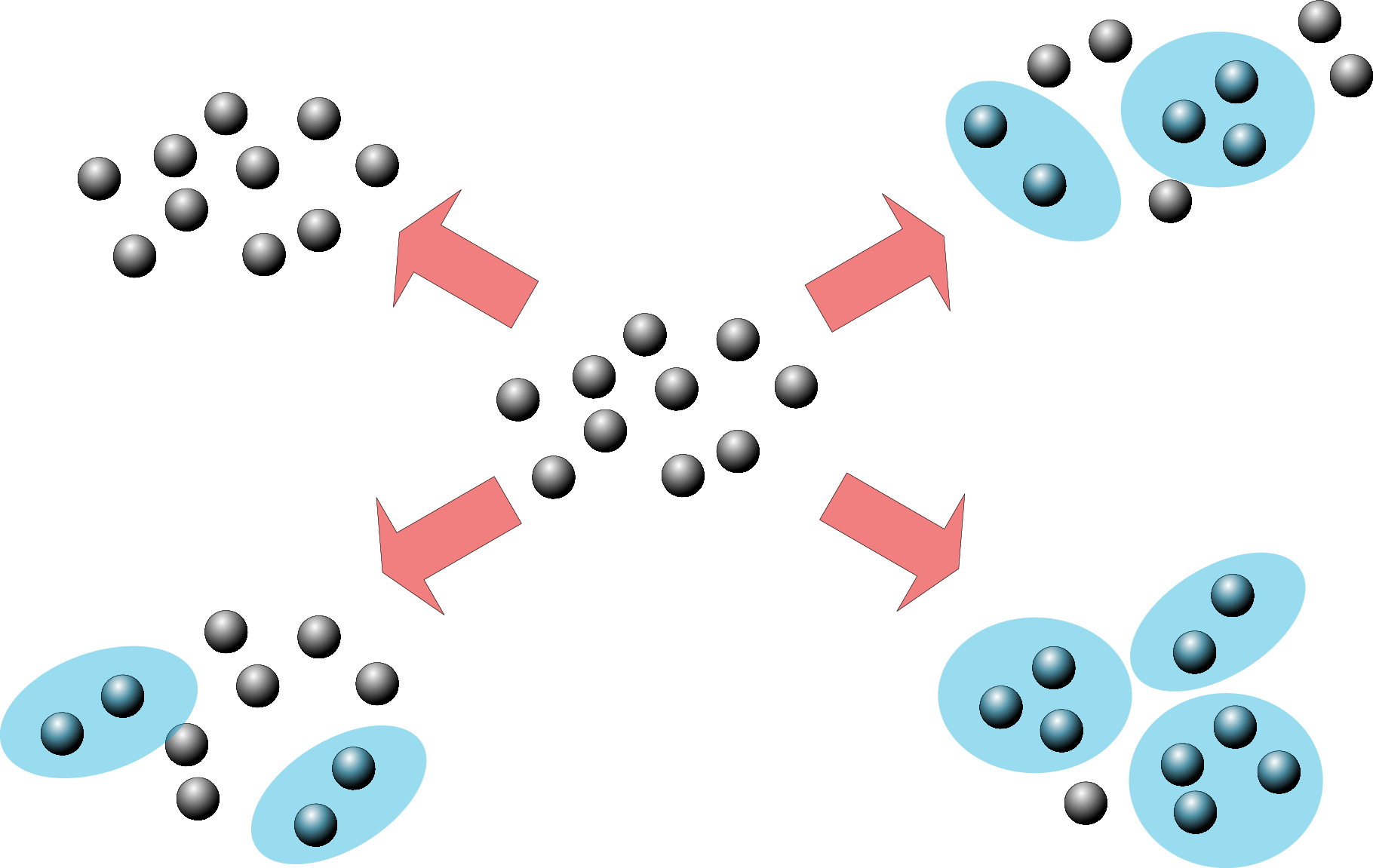
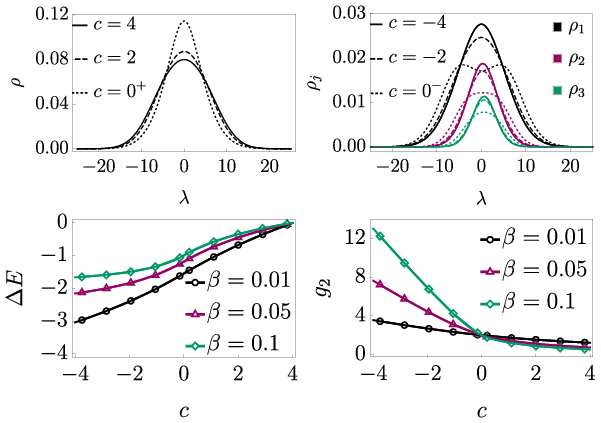
Adiabatic formation of bound states in the 1d Bose gas
Phys. Rev. B 103, 165121 (2021)

Conclusions and perspectives
- Integrable models as a basis for renormalization: without doubt a good idea
- Ordering by energy is demonstrably suboptimal
- Order(s?) of magnitude improvements in computational efficiency obtainable by using more refined measures $\rightarrow$ new take on RG
- Generalized hydrodynamics: adiabatic behaviour
Hubert: thank you.
Happy Birthday!
