Out-of-equilibrium quantum matter
Successes, challenges, and opportunities
Nano, Quantum and Materials Physics (NQMP) community day
Nijmegen, 24 June 2025Jean-Sébastien Caux




Plan of the talk
Out-of-equilibrium: why?
Why NOT?
- Real systems equilibrate very rapidly
- Experimentally: tough to control
- Theoretically: can't do it - toolbox too limited
Why INDEED?
- Real isolated systems can equilibrate slowly
- Novel states & properties
- Experimentally: frontier of current capabilities
- Theoretically: the toughest challenge around?
Mechanical
motivation
Out of equilibrium: terminology
Out of equilibrium: what? how?
- Neutron scattering
- Bragg spectroscopy
- Transport
- Linear response
- Traditional methods
- CFT, Bosonization, ...
- Magnetic resonance
- Photoemission
- Ultrafast spectr.
- Free models
- Numerics
- Nonlinear response theory
- Feshbach resonances
- Integrability
- Hydrodynamics ($t\rightarrow \infty$)
- GGE ($t = \infty$)
- Quench Action ($\forall t$)
- Masers/lasers
- Resonators
- Free models
- Floquet theory
- Numerics
- Despair?
Out-of-equilibrium using Integrability
- Split Fermi seas (Moses states)
- Spin echo in quantum dots
- Quasisolitons
- The super Tonks-Girardeau gas
- Interaction quench in Richardson
- Domain wall release in Heisenberg
- Geometric quench
- Interaction cutoff in Lieb-Liniger
- Release of trapped Lieb-Liniger
- BEC to Lieb-Liniger quench
- Quantum Newton’s Cradle in TG
- Néel to XXZ quench
- Generalized hydrodynamics
- Floquet driven spin chains
Quantum Gases
The Lieb-Liniger Model
$ H = \int_0^L dx \left[ \partial_x \Psi^{\dagger}(x) \partial_x \Psi(x) + c \Psi^{\dagger} (x) \Psi^{\dagger}(x) \Psi(x) \Psi(x) \right] $
Eigenstates: Bethe Ansatz
\[ \begin{align} \Psi_N(\{ x \} | \{ \lambda \}) &= \prod_{N \geq j_1 > j_2 \geq 1} sgn(x_{j_1} - x_{j_2}) sgn (\lambda_{j_1} - \lambda_{j_2}) \times \\ &\times \sum_{P \in \pi_N} (-1)^{[P]} e^{i \sum_{j=1}^N \lambda_{P_j} x_j + \frac{i}{2} \sum_{N \geq j_1 > j_2 \geq 1} sgn(x_{j_1} - x_{j_2}) \phi (\lambda_{P_{j_1}} - \lambda_{P_{j_2}})} \end{align} \]
in which $\phi(\lambda) \equiv 2\mbox{atan}(\lambda/c)$
The Lieb-Liniger Model
(Dynamical) Correlation functions
\[ {\cal S}^{a \bar{a}} (k, \omega) \equiv \frac{1}{N} \sum_{j, j'} e^{-i k(j-j')} \int_{-\infty}^\infty dt e^{i\omega t} \langle \frac{1}{2} \left[ {\cal O}^a_j (t), ({\cal O}^a_{j'} (0))^\dagger \right] \rangle \]
Simplest examples:
- Dynamical structure factor: ${\cal O}_j = \rho_j \equiv \Psi^\dagger(x_j) \Psi(x_j)$
- One-body function (Green's): ${\cal O}_j = \Psi(x_j)$ or $\Psi^\dagger(x_j)$
Dynamical structure factor
from (algebraic) Bethe Ansatz

Abacus (post Achilles)
Dynamical structure factor
from (algebraic) Bethe Ansatz
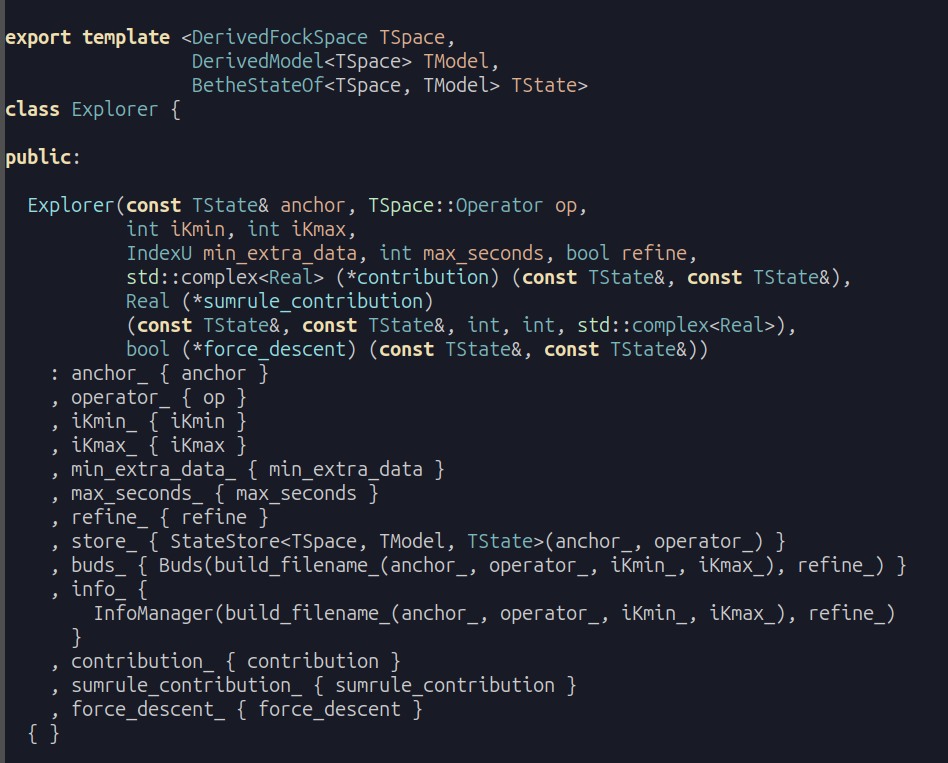
The ABACUS algorithm
Dynamical structure factor from Bethe Ansatz
extension to finite TM. Panfil and J-SC, PRA 89 (2014)
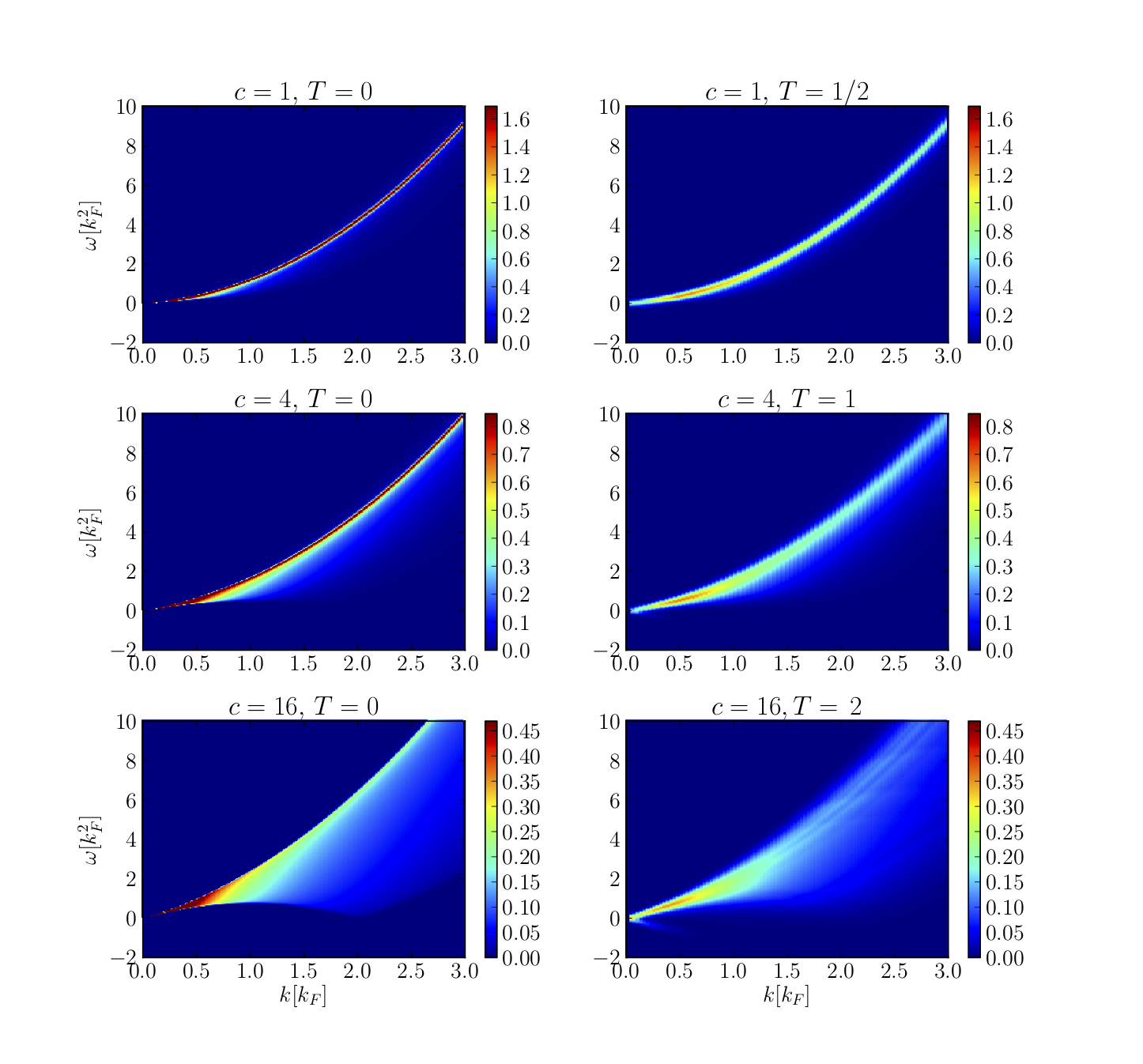
Lieb-Liniger using cold atoms (I)

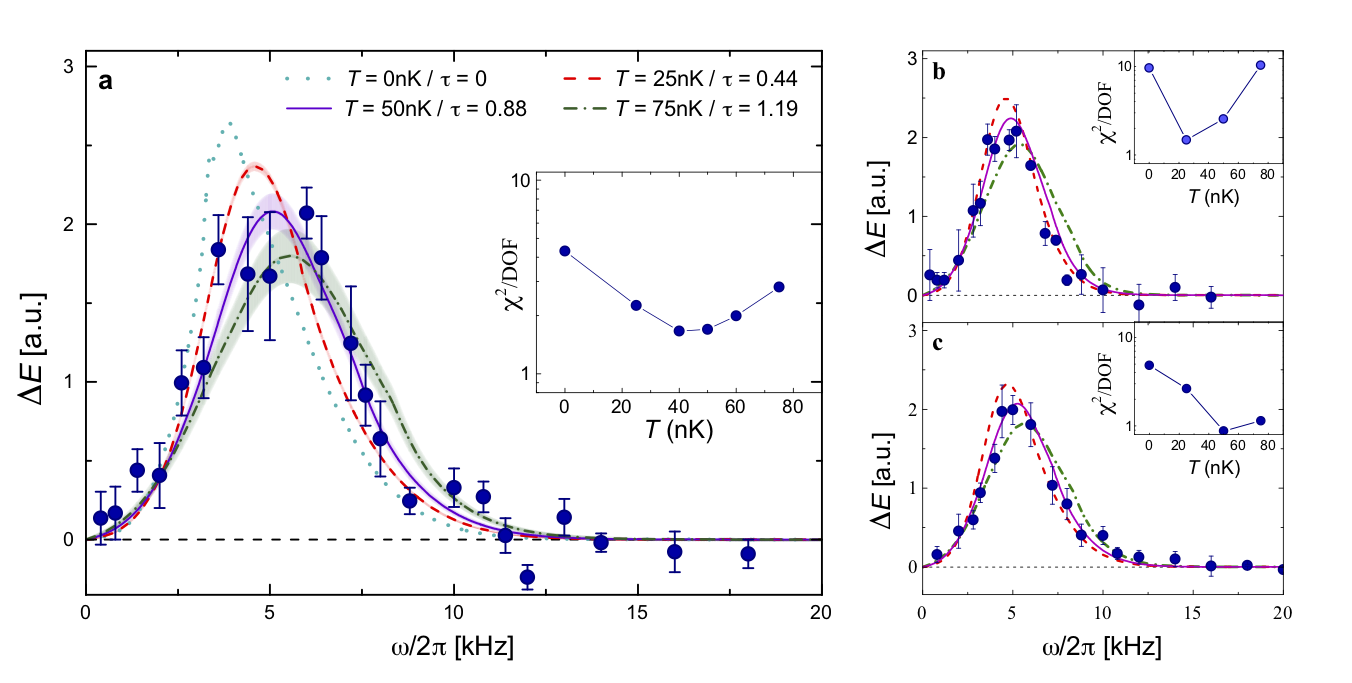
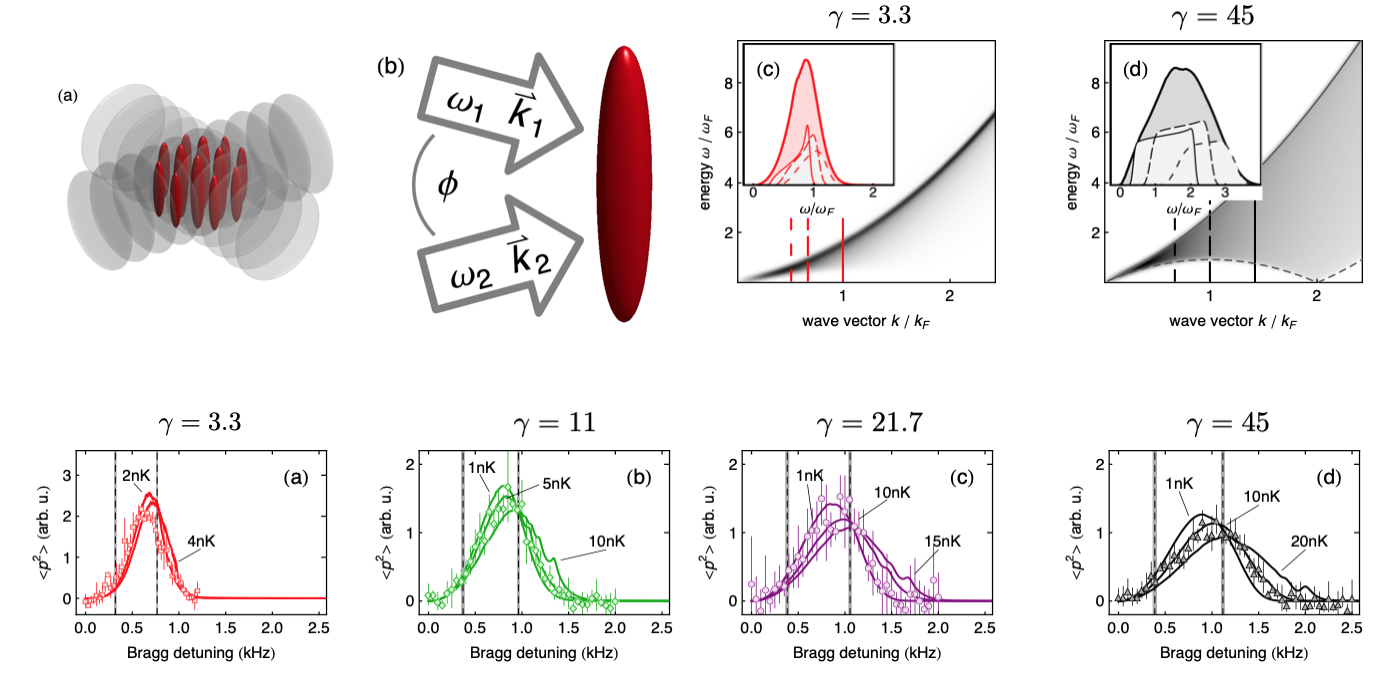
Lieb-Liniger using cold atoms (II)

Let's

Interaction quench in Lieb-Liniger
We will consider a sudden switch of the interaction:
$ c (t) = \left\{ \begin{array}{ll} c_i & t < 0, \\ c_f & t > 0 \end{array} \right. $
starting in ground/(any eigen)state of $H(c_i)$ at $t < 0$
For many reasons, this is a complicated problem...
Exact solution using Quench Action
$ S^Q = L\int_0^\infty d\lambda \rho(\lambda) \log\left(\frac{\lambda^2}{c^2} \left( \frac{1}{4} + \frac{ \lambda^2}{c^2} \right) \right) + S^{YY} $
Saddle-point equation:
$ \ln \eta(\lambda) = g(\lambda) - h - \int_{-\infty}^\infty \frac{d\lambda'}{2\pi} K (\lambda - \lambda') \ln \left[ 1 + \eta^{-1}(\lambda') \right], $
with driving term $ g(\lambda) = \ln \left[ \frac{\lambda^2}{c^2} \left( \frac{\lambda^2}{c^2} + \frac{1}{4} \right) \right] $
Analytic solution for steady state:
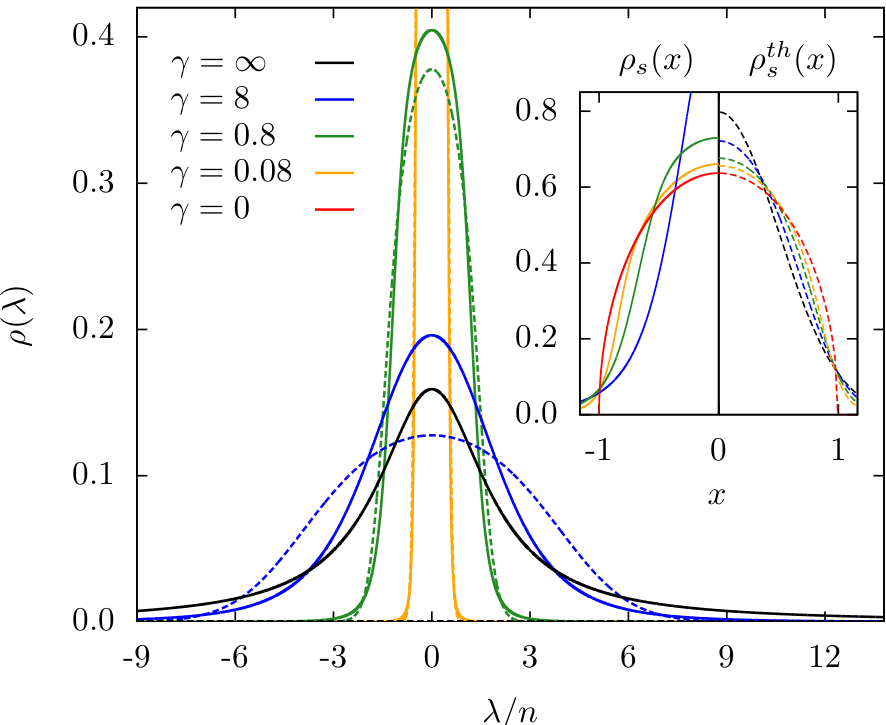
$ \begin{align} \rho_{sp} (\lambda) &= -\frac{\gamma}{4\pi} \frac{1}{1 + a(\lambda)} \frac{\partial a(\lambda)}{\partial \gamma},\\ a(\lambda) &\equiv \frac{2\pi}{\frac{\lambda}{n} \sinh \frac{2\pi \lambda}{c}} I_{1 - 2i\frac{\lambda}{c}} \left(\frac{4}{\sqrt{\gamma}}\right) I_{1 + 2i\frac{\lambda}{c}} \left(\frac{4}{\sqrt{\gamma}}\right) \end{align} $
Exact solution using Quench Action
Steady state distribution: non-thermal
J. De Nardis, B. Wouters, M. Brockmann & J-SC, PRA 89, 2014
Generalized Hydrodynamics
Quenches from spatially inhomogeneous states
- B. Bertini, M. Collura, J. De Nardis and M. Fagotti, PRL 117, 207201 (2016)
- O. A. Castro-Alvaredo, B. Doyon and T. Yoshimura, PRX 6, 041065 (2016)
- B. Doyon and T. Yoshimura, SciPost Phys. 2, 014 (2017)
After initial dephasings:
'hydrodynamic' evolution
described by local GGE
$\partial_t \rho (\lambda) + \partial_x (v^{\tiny \mbox{eff}}(\lambda) \rho (\lambda)) = 0$
with effective velocities determined by the dressing equation
Effective dynamics:
"flea gas" of scattering quasiparticles
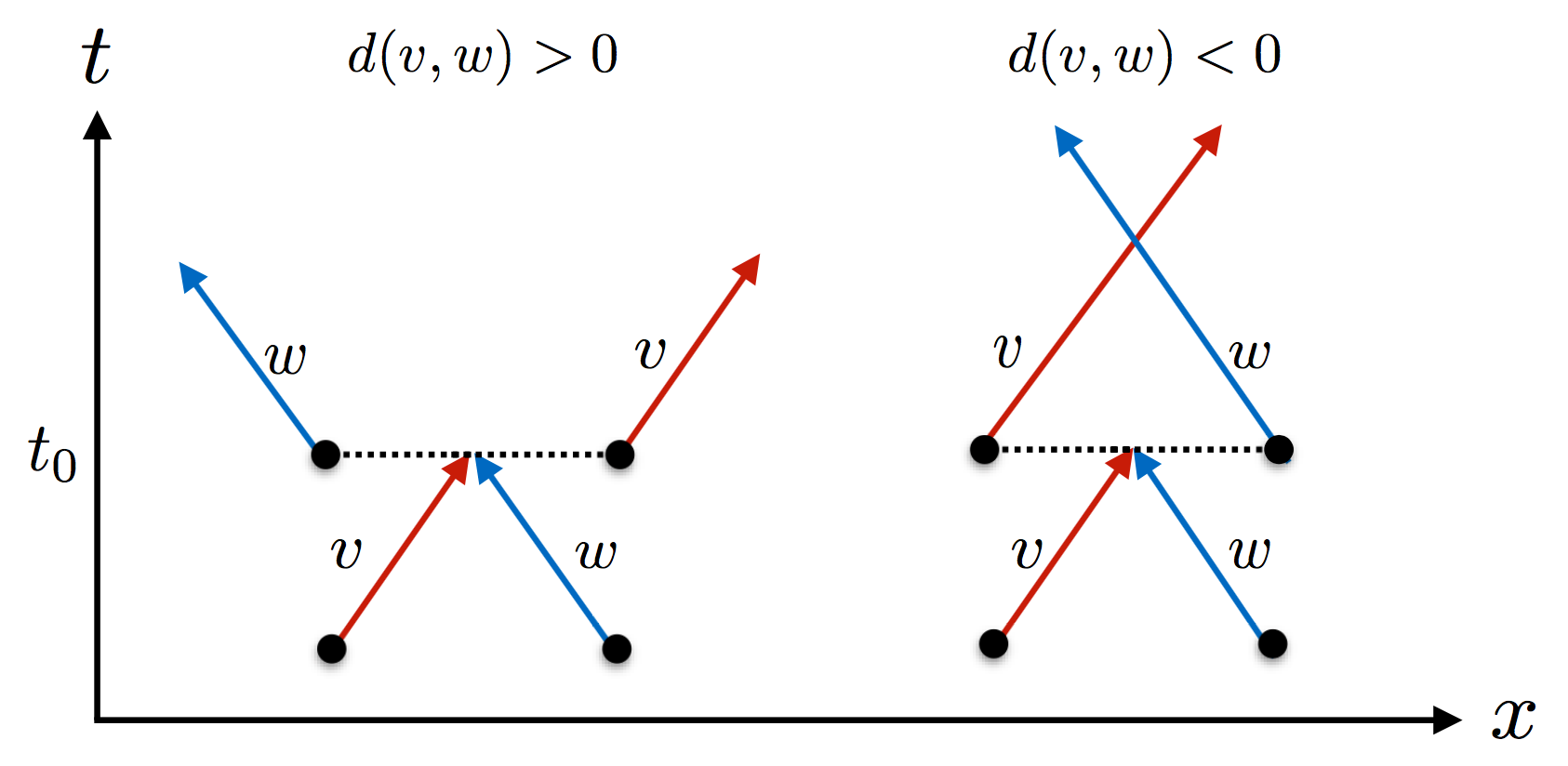
Flea gas GHD
for the Quantum Newton's Cradle
JSC, B. Doyon, J. Dubail, R. Konik and T. Yoshimura, SciPost Phys. 6, 070 (2019)
Short time scales:
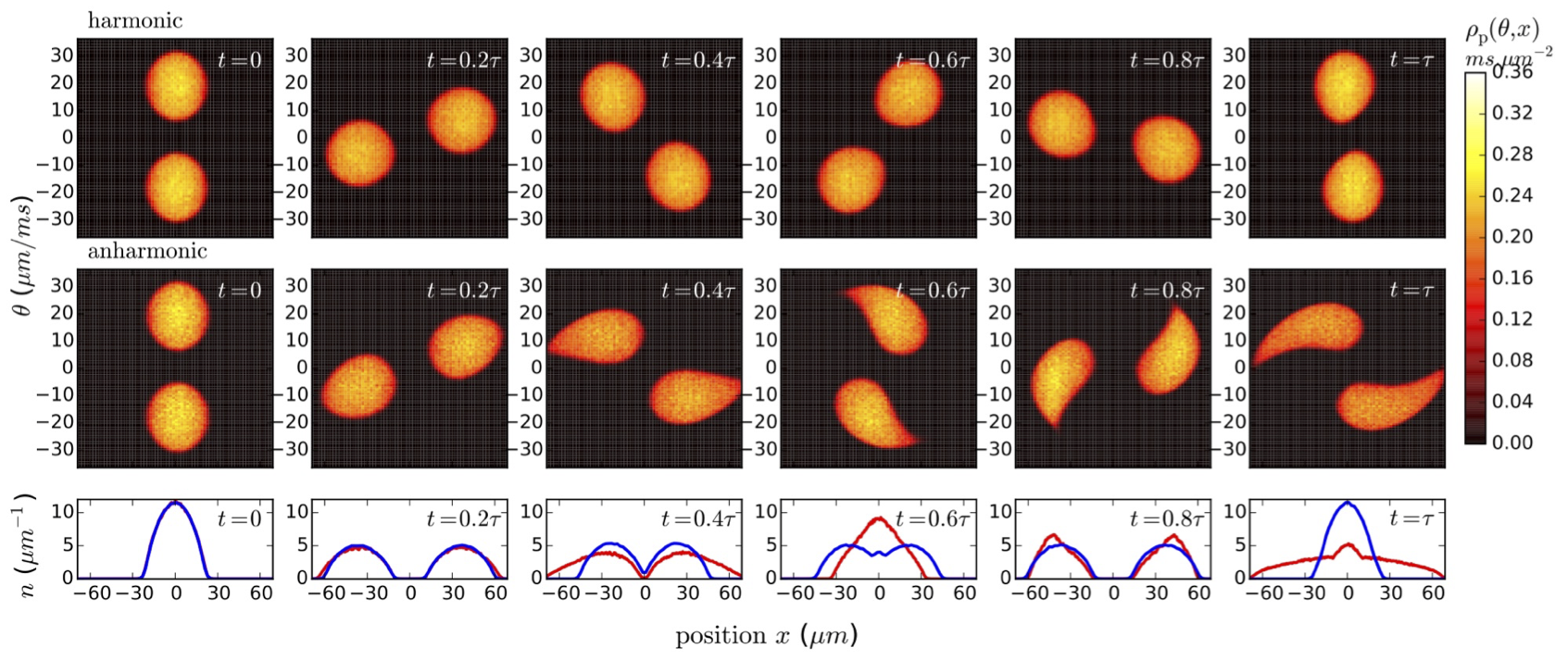
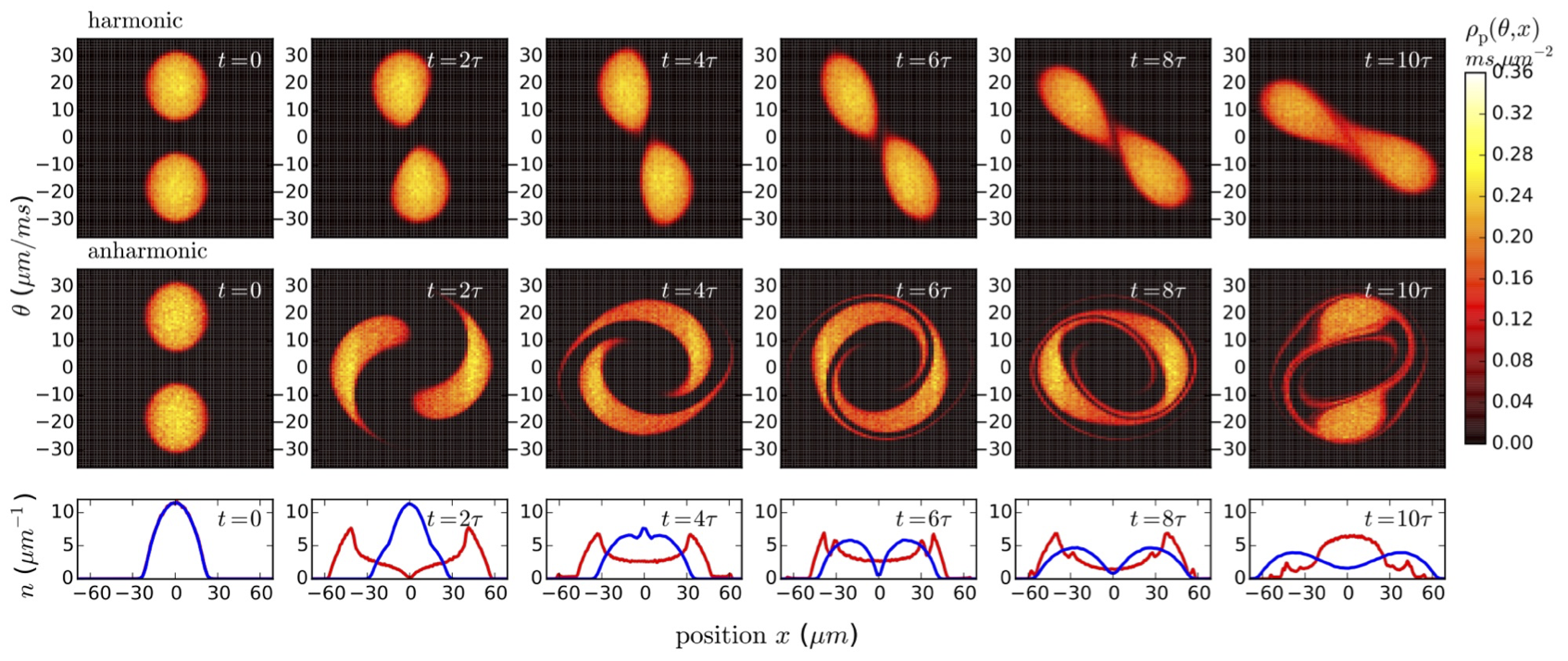
Flea gas GHD
for the Quantum Newton's Cradle
JSC, B. Doyon, J. Dubail, R. Konik and T. Yoshimura, SciPost Phys. 6, 070 (2019)
Longer time scales:
Generalized Hydrodynamics with space/time-dependent potentials
Phys. Rev. Lett. 123, 130602 (2019)


Adiabatic formation of bound states in the 1d Bose gas
Phys. Rev. B 103, 165121 (2021)

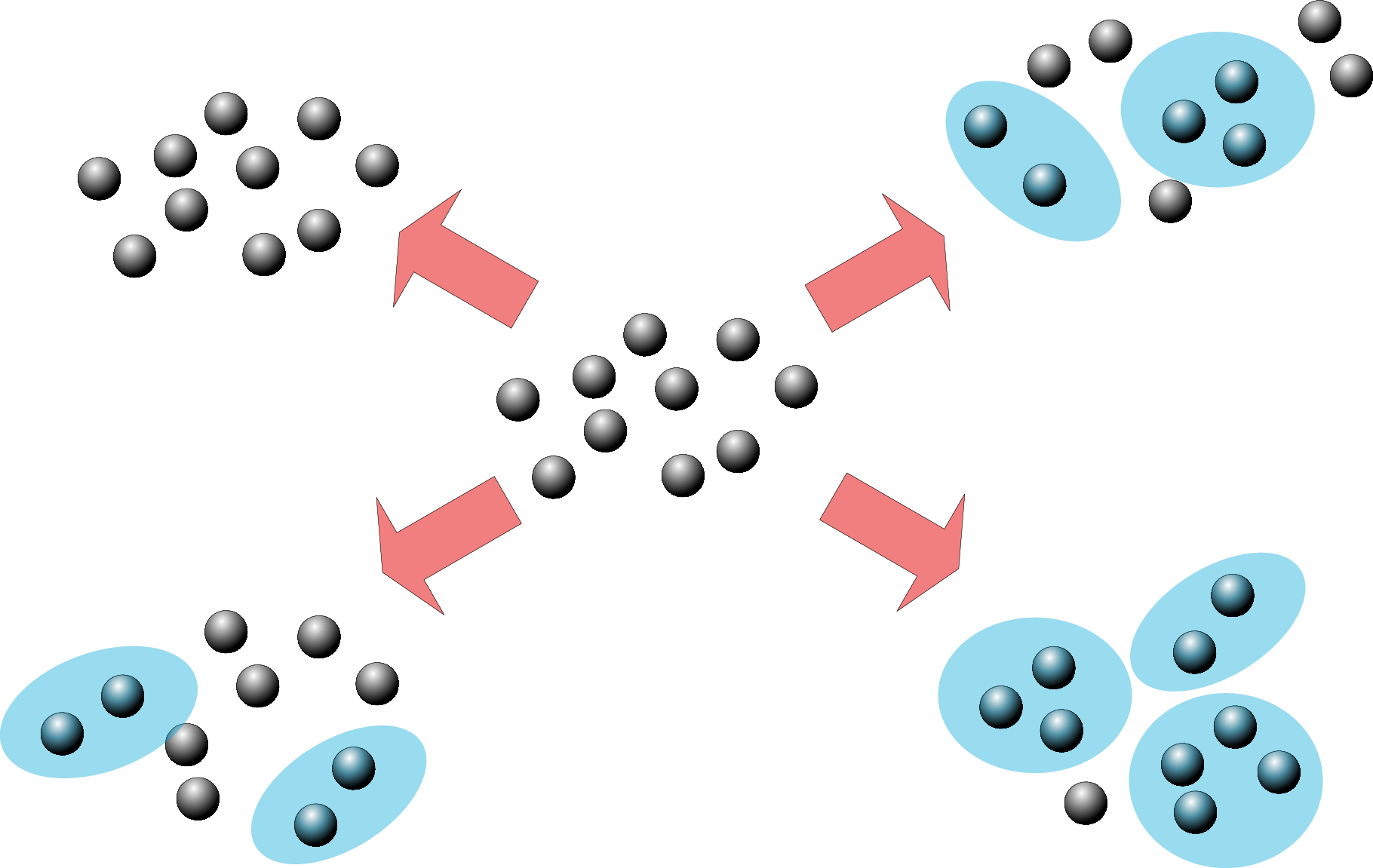
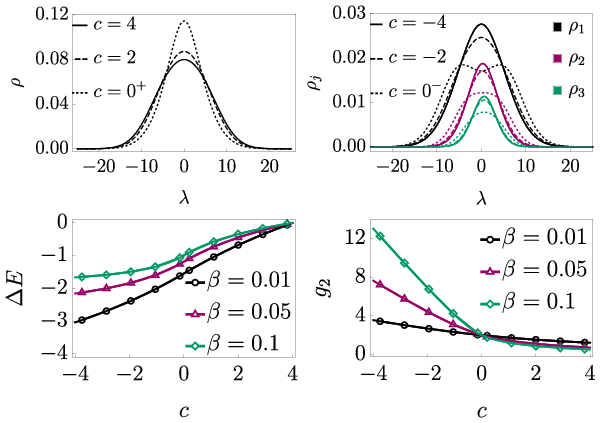
Observing Bethe strings in an attractive Bose gas far from equilibrium
Milena Horvath, Alvise Bastianello, Sudipta Dhar, Rebekka Koch, Yanliang Guo,
Jean-Sébastien Caux, Manuele Landini, and Hanns-Christoph Nägerl, arXiv:2505.10550
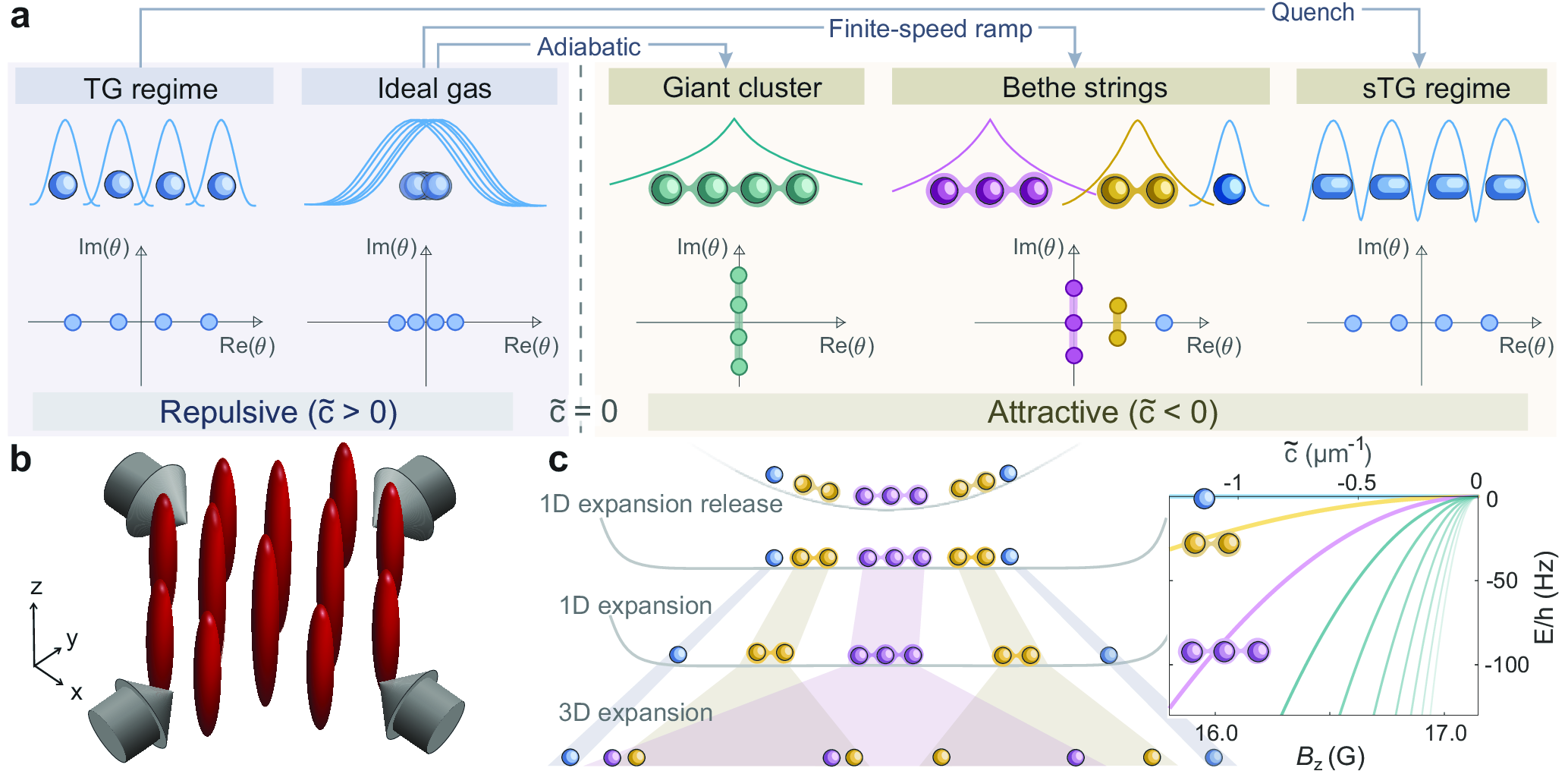
Observing Bethe strings in an attractive Bose gas far from equilibrium
Milena Horvath, Alvise Bastianello, Sudipta Dhar, Rebekka Koch, Yanliang Guo,
Jean-Sébastien Caux, Manuele Landini, and Hanns-Christoph Nägerl, arXiv:2505.10550
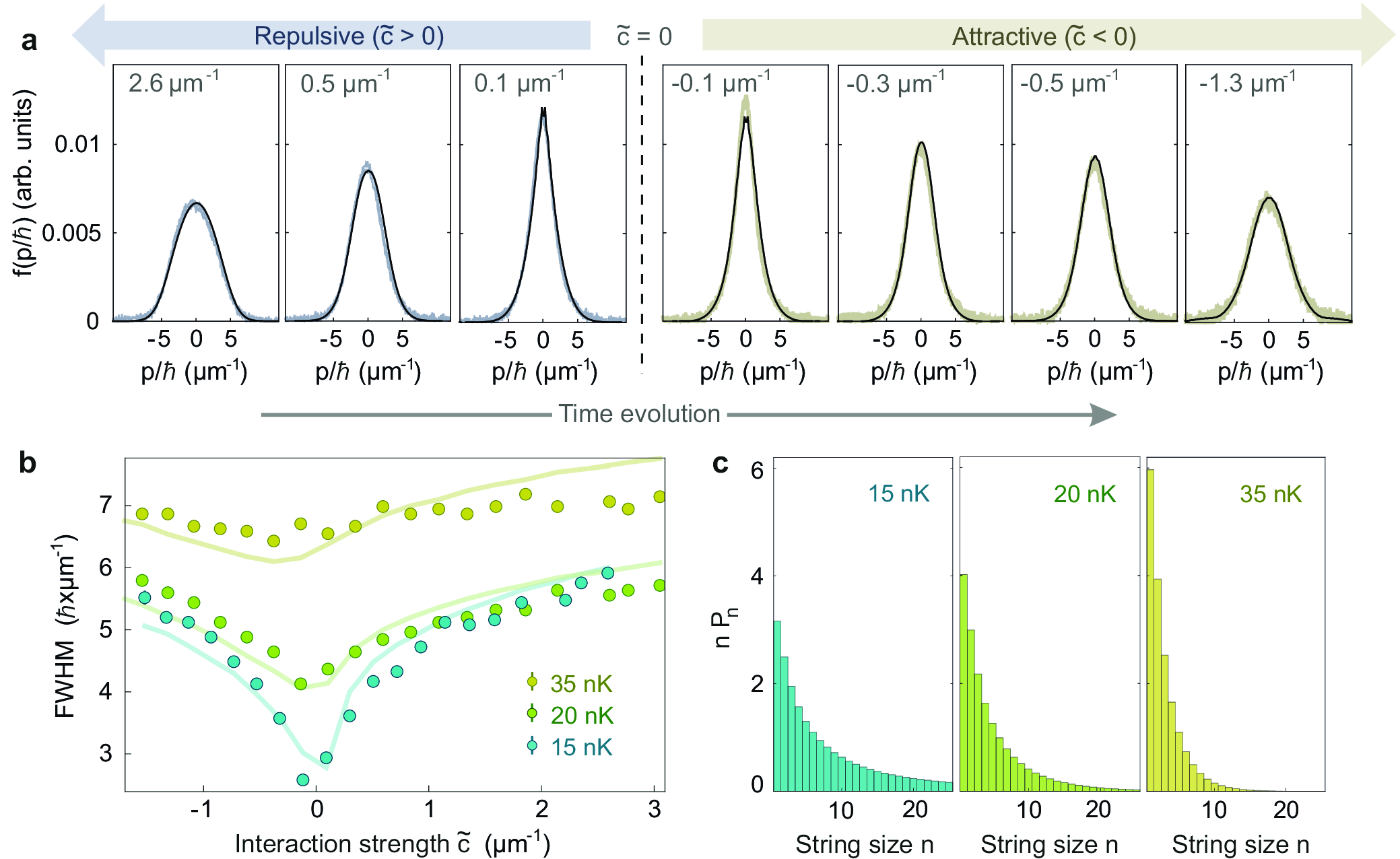
Quantum Spin Chains
The structure factor
of the Heisenberg chain
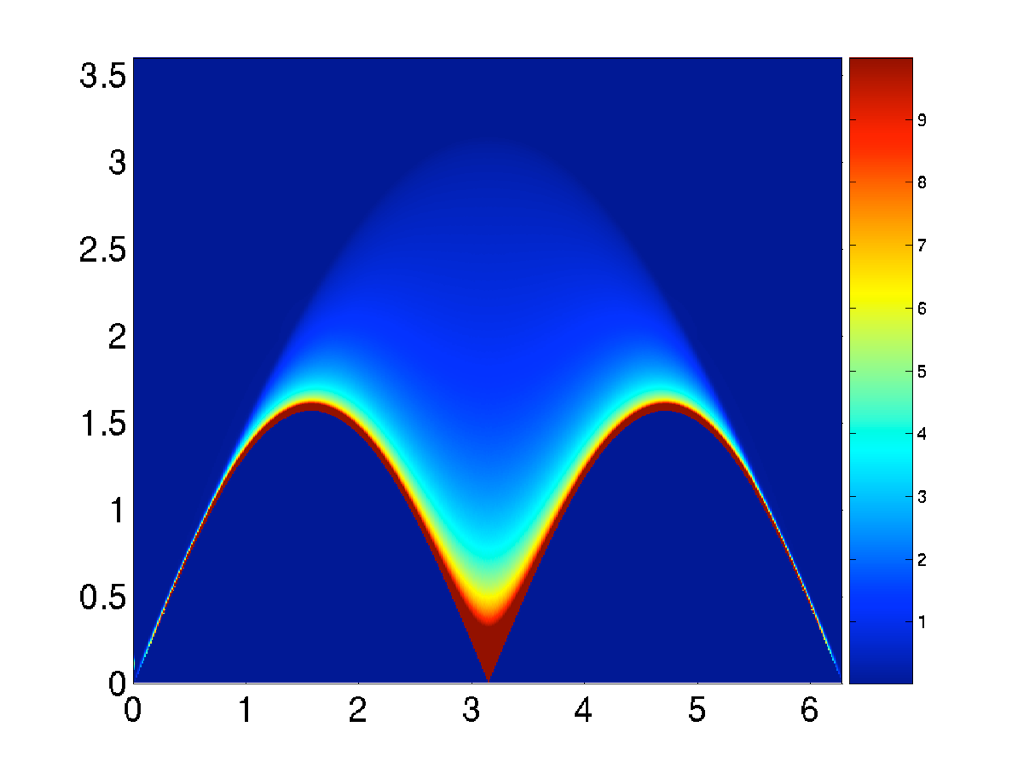
Quantum wake dynamics in Heisenberg
A. Scheie, P. Laurell, B. Lake, S. E. Nagler, M. B. Stone, JSC, D. A. Tennant
Nature Communications 13, 5796 (2022)
- Inelastic neutron scattering on $K Cu F_3$
- Really accurate data in momentum/frequency space enabling...
- Fourier transform to real space / time
- Look specifically at high-energy features
Quantum wake dynamics in Heisenberg
A. Scheie, P. Laurell, B. Lake, S. E. Nagler, M. B. Stone, JSC, D. A. Tennant
Nature Communications 13, 5796 (2022)
- Quantum wake:
a local, coherent, long-lived, quasiperiodically oscillating magnetic state emerging out of the distillation of propagating excitations following a local quantum quench
Quantum wake dynamics in Heisenberg
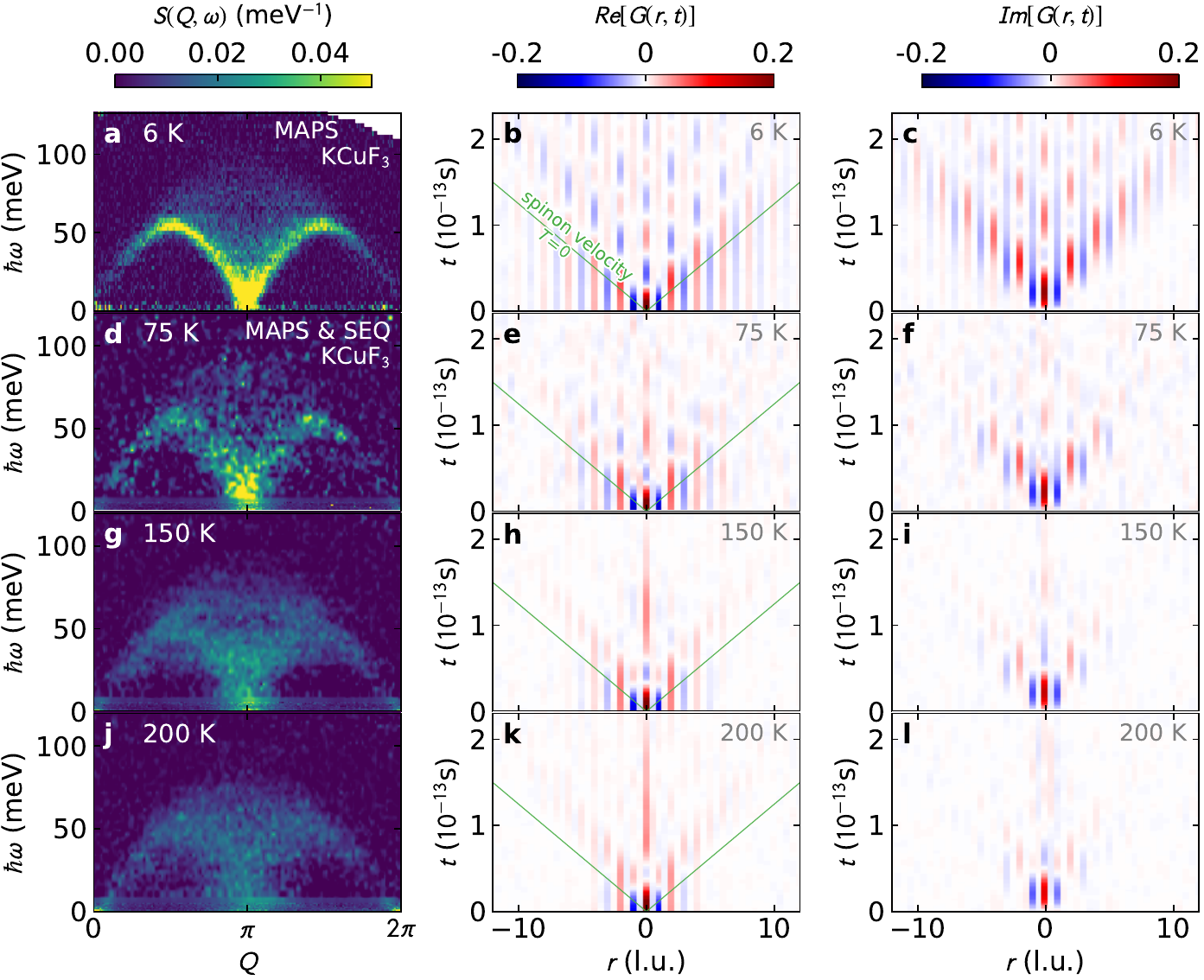
Quantum wake dynamics in Heisenberg
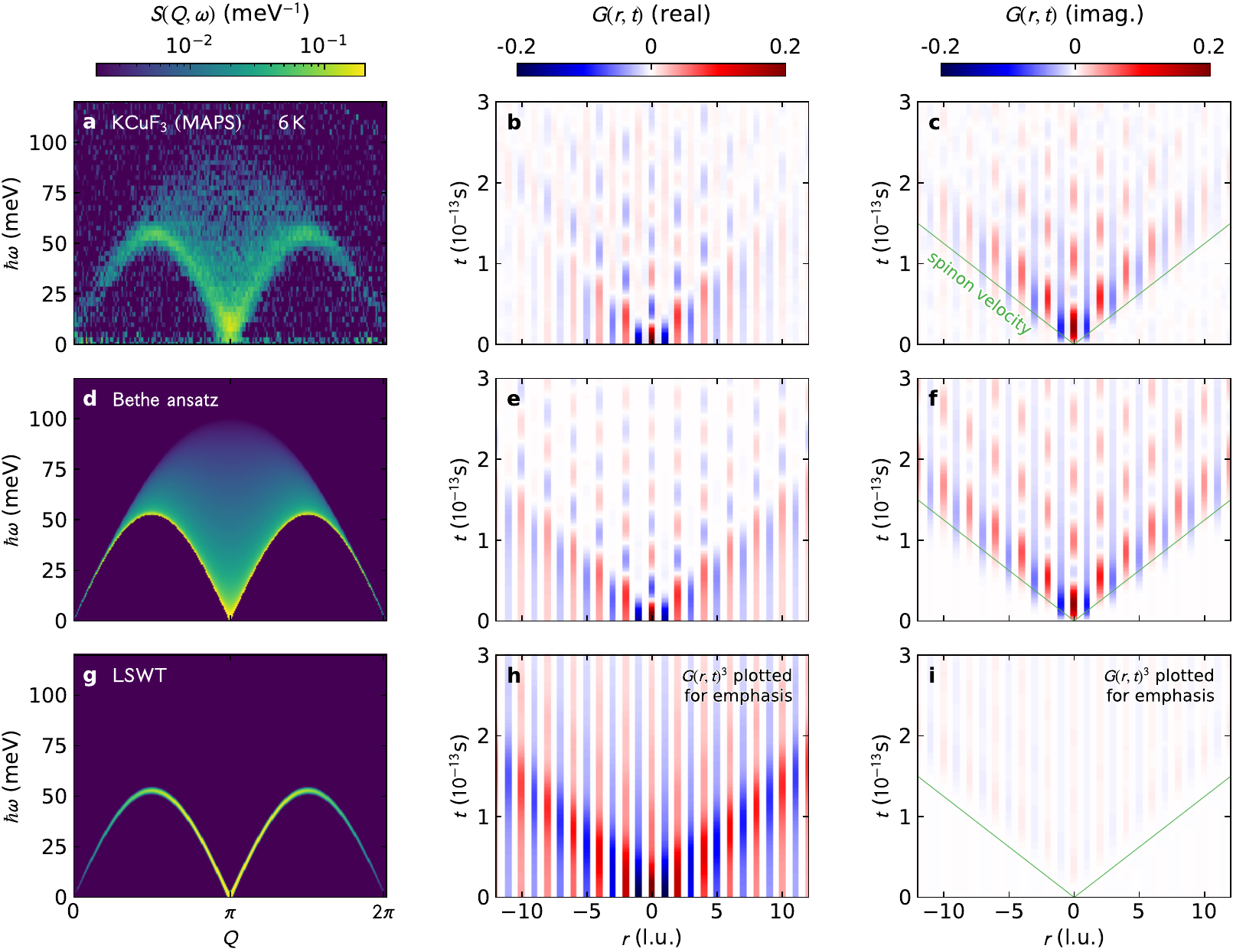
Quantum wake dynamics in Heisenberg
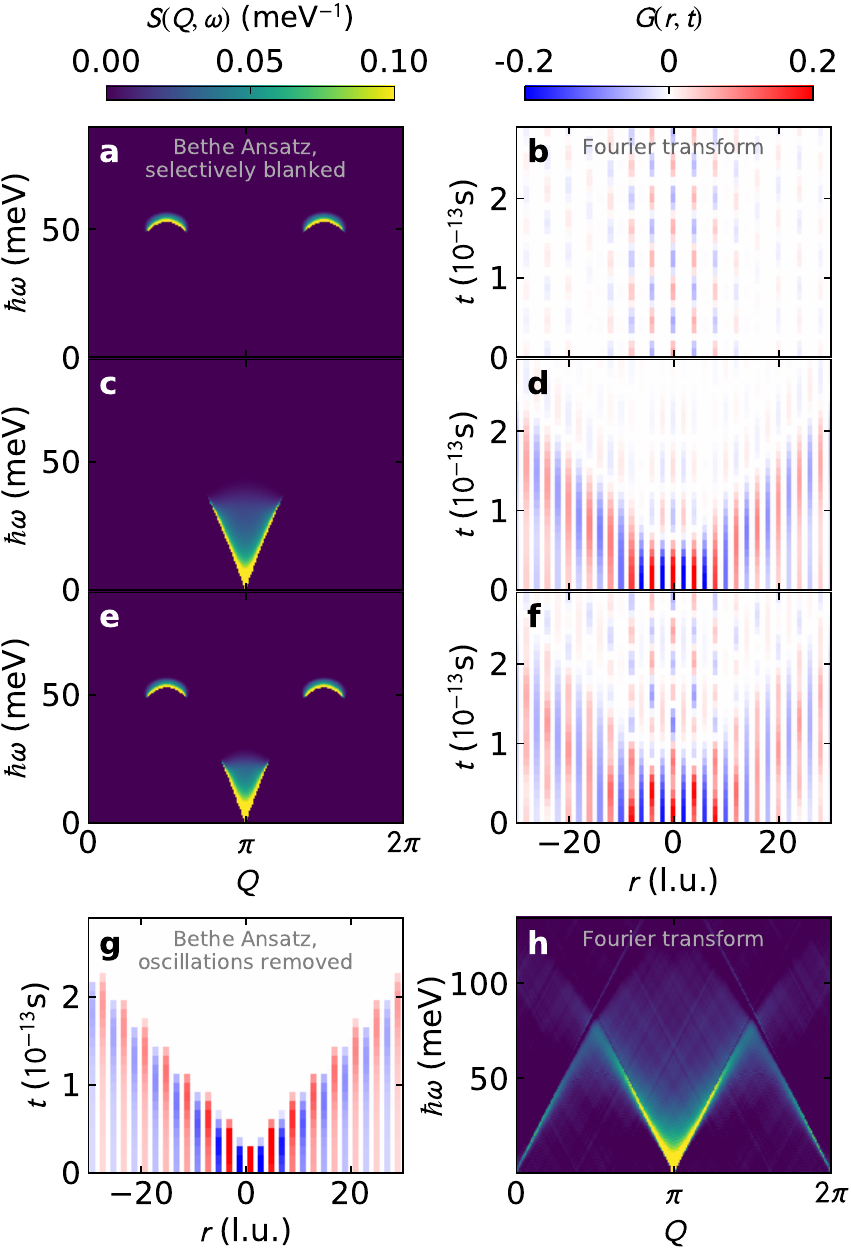
Selectively (patch-wise) Fourier transforming: $k=\pi/2$ (mod $2\pi$) states are responsible for the quantum wake dynamics
Beyond the reach of any low-energy method
Not mentioned here
- Renormalization from integrability
- (Nonlinear) Luttinger liquids
- Lessons for field theory
- "Bethe liquid theory"
- Quasisolitons in quantum gases
Challenges and Opportunities
- Detailed phenomenology for quantum gases
- Transport: (sub/super)diffusion
- Ultrafast magnetism
- Central spin / NV centers
- Floquet dynamics
- Driven dissipative systems
- Quantum circuits