Electrodynamics

a (re)introduction

Jean-Sébastien Caux

"Classical" electrodynamics is boring because

it's a dead subject (it hasn't changed much in the last 100 years)
we've studied it before, we know everything already
there are much more interesting forces in nature

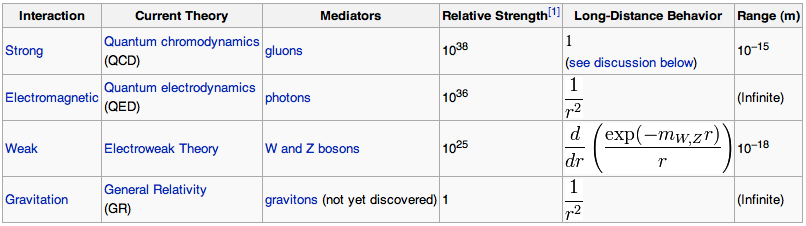
Interesting historical anecdotes

Galvani (1780s)

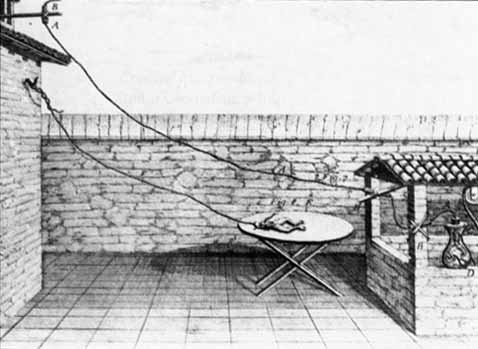
Interesting historical anecdotes

Aldini (1800s)

Interesting historical anecdotes

Nijmegen (2000s)

Electrodynamics giving "life"

or death

Energetics of fission reaction: U-235

kinetic energy of neutrons	\(\sim 2\) MeV
gamma ray photons	\(\sim 7\) MeV
kinetic energy of nuclei	\(\sim 170\) MeV

Nuclei fly apart at about 3% of light speed
because of Coulomb repulsion

Important aspects of electric charges and classical electrodynamics

charge comes in two different varieties (+ and -)
charge is quantized in discrete units
charge is conserved (locally)
force has inverse square form
forces display linear superposition

Elementary charge: how accurately is it known?

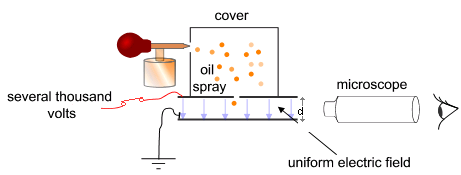
Simplified_scheme_of_Millikan’s_oil-drop_experiment.png

Theresa Knott, CC BY-SA 3.0, via Wikimedia Commons

Millikan's oil droplet experiment (1909; Nobel 1923):

\(1.5924(17) \times 10^-19\) C (accurate to 1% of current value)

Most accurate way of measuring \(e\)

combine the…

Josephson effect (voltage to frequency)

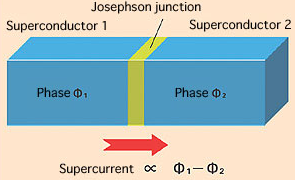
\(I(t) = I_c \sin \phi(t)\), \(\frac{d\phi}{dt} = \frac{\hbar}{2e} V(t)\)

and the…

Quantum Hall effect

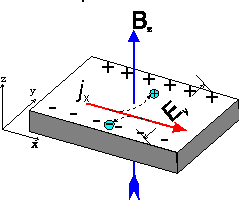
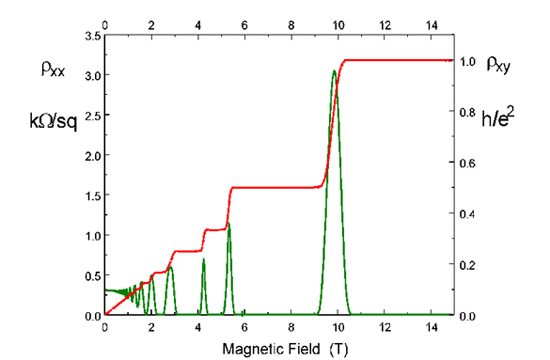
Together: \(2 \times \frac{h}{2e} \times \frac{e^2}{h} = e = 1.602176487(40) \times 10^{-19} C\)

How accurately is charge quantized?

Published experiments: \(\frac{|e_{el}| - e_p|}{|e_{el}|} \lesssim 10^{-21}\)

Proposed experiment using cold atoms, lasers and interferometry: \(\frac{|e_{el}| - e_p|}{|e_{el}|} \lesssim 10^{-28}\)

How accurate is Coulomb's law?

Possible deviations:

the force is not \(\frac{1}{r^2}\) but \(\frac{1}{r^{2 + \epsilon}}\)
the potential has a Yukawa form, \(\frac{e^{-\mu r}}{r}\) where \(\mu = m_\gamma c/\hbar\) ('massive' photon)

Tests of exponents throughout the ages

Cavendish's experiment

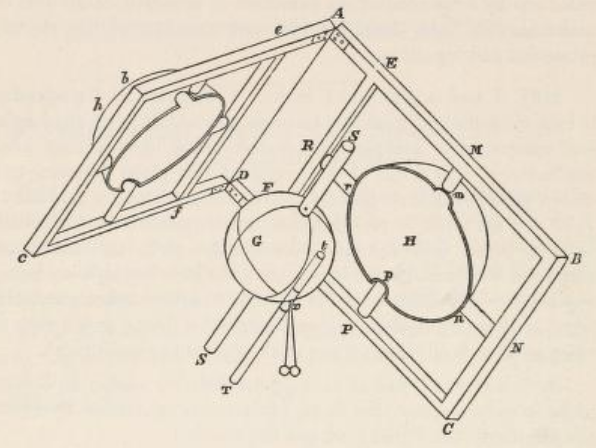
See the account of Cavendish's extraordinary work, by none other that J. C. Maxwell, in The electrical researches of the Honourable Henry Cavendish

Most quoted "recent" experiment

Williams, Faller, Hill 1971

\(\epsilon = (2.7 \pm 3.1) \times 10^{-16}\)

Revisited by Fulcher (1986):

\(\epsilon = (1.0 \pm 1.2) \times 10^{-16}\)

Willimans Faller Hill 1971

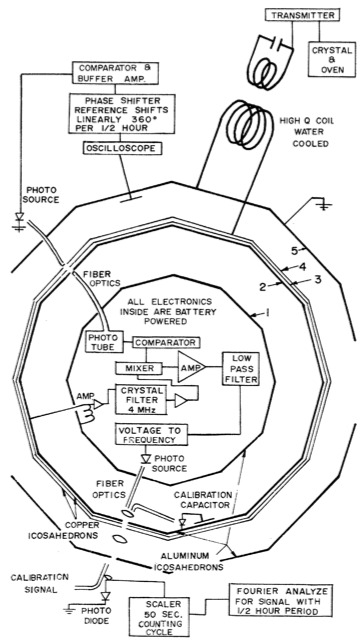
Tests of the photon mass

terrestrial measurements of \(c\) at different frequencies
measurement of radio dispersion in pulsar signals
lab tests of Coulomb's law
limits on constant external magnetic field at Earth's surface (Schrödinger!)

Tests of the photon mass (recent)

Could exist down to a scale given by Heisenberg's uncertainty principle: (age of universe \(\simeq 10^{10}\) years)

\(m_\gamma \simeq \frac{\hbar}{(\Delta t) c^2} \simeq 10^{-66} g\)

Is the electron really a point-like particle?

Suppose that it is. Problem: field energy diverges!

\[ u = \frac{\varepsilon_0}{2} E^2 = \frac{e^2}{32 \pi \varepsilon_0 r^4} \] \[ \rightarrow U = \int dr \frac{e^2}{8 \varepsilon_0 r^2} \rightarrow \infty \]